Введение
В этой статье я бы хотел затронуть такую важную и фундаментальную тему для любого программиста, как числа с плавающей точкой. На данную тему уже написано большое количество статей, однако многие из них используют пугающие математические формулы и нотации, что может быть сложно для понимания новичкам.
В этой статье я простым языком попытаюсь изложить данную тему и помочь решить ряд вопросов: как на самом деле процессор хранит числа с плавающей точкой? Как точка хранится в памяти? Почему при сложении 0.1 + 0.2 получается ответ ~0.30000000000000004? Если по какому-то из этих вопросов вы чувствуете, что не можете дать точный ответ, то эта статья для вас.
Важное замечание: в этой статье не будут рассмотрены все "тонкие моменты" работы чисел с плавающей точкой. Цель этой статьи - дать фундаментальные знания новичкам в программировании о том, как с этими числами взаимодействует процессор.
Немного истории
В далекие 60-70-ые годы не было единого стандарта для представления чисел с плавающей точкой, что создавало трудности для программистов. Каждая линейка компьютеров того времени работала по-разному. В зависимости от процессора, числа с плавающей точкой имели разную точность и округлялись по-разному. Например, при умножении числа на 1.0 число могло потерять последние 4 бита точности или два числа при вычитании могли вернуть ноль, при этом числа были не равны друг другу. Даже некоторые игры того времени, которые были написаны под определенные модели видеокарт, не работали на других моделях, потому что "железо" по-разному обрабатывало числа с плавающей точкой. Для многих это была проблема.
Тогда в 1976 году компания Intel решила разработать собственный сопроцессор для работы с плавающей точкой для своих микропроцессоров i8086/8. Разработкой курировал профессор Джон Палмер. В процессе работы именно он убедил Intel в том, что им нужен свой стандарт для решения этого вопроса. Палмер пригласил своего знакомого Вильяма Кэхэна, который первое время выступал как консультант, но в последствии принимал непосредственное участие в работе над стандартизацией. Конкурентами Intel в вопросах стандартизации выступали и другие именитые компании, такие как Zilog, DEC, Motorola. В конечном итоге среди общих стандартов были выбраны 2: VAX от DEC и K-C-S от Intel. Intel до последнего держала в тайне алгоритмы декодирования чисел с плавающей точкой, однако в ходе баталий была вынуждена раскрыть некоторые секреты спецификации устройства и алгоритмов вычисления, что позволило занять главенствующую позицию, и их стандарт был утвержден.
Данный стандарт впоследствии получил название IEEE-754. Он описывает способ хранения и работы чисел с плавающей точкой, который, казалось бы, раз и навсегда решил все проблемы, связанные с этим типом чисел. Однако, давайте разберемся, действительно ли это так.
Перевод из десятичной системы счисления в двоичную
Для начала стоит отметить, что для процессора на самом деле не существует точки: она видна только в конечном итоге визуально при вводе данных или отображении числа на экране. Но раз процессор не знает, что такое точка, как он понимает, когда и где нам нужно ее поставить? Разработчики стандарта IEEE-754 начали думать, как решить эту проблему, и в итоге столкнулись с неидеальностью нашей системы исчисления и математики в целом, которую не удалось решить до сегодняшнего дня.
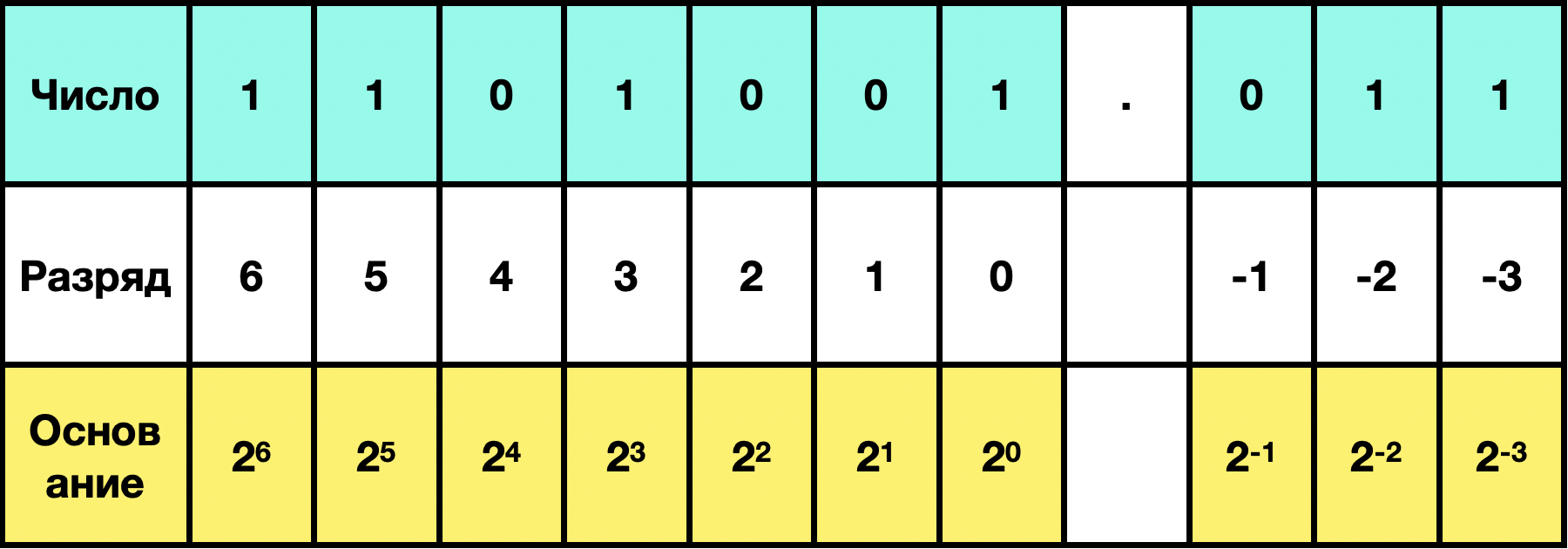
Для начала разберемся, как устроены дробные числа в математике в двоичной и десятичной системах, не затрагивая память компьютера. Рассмотрим на примере числа 105.375. По-другому это число можно записать как 1*102 + 0*101 + 5*100 + 3*10-1 + 7*10-2 + 5*10-3 = 105.375
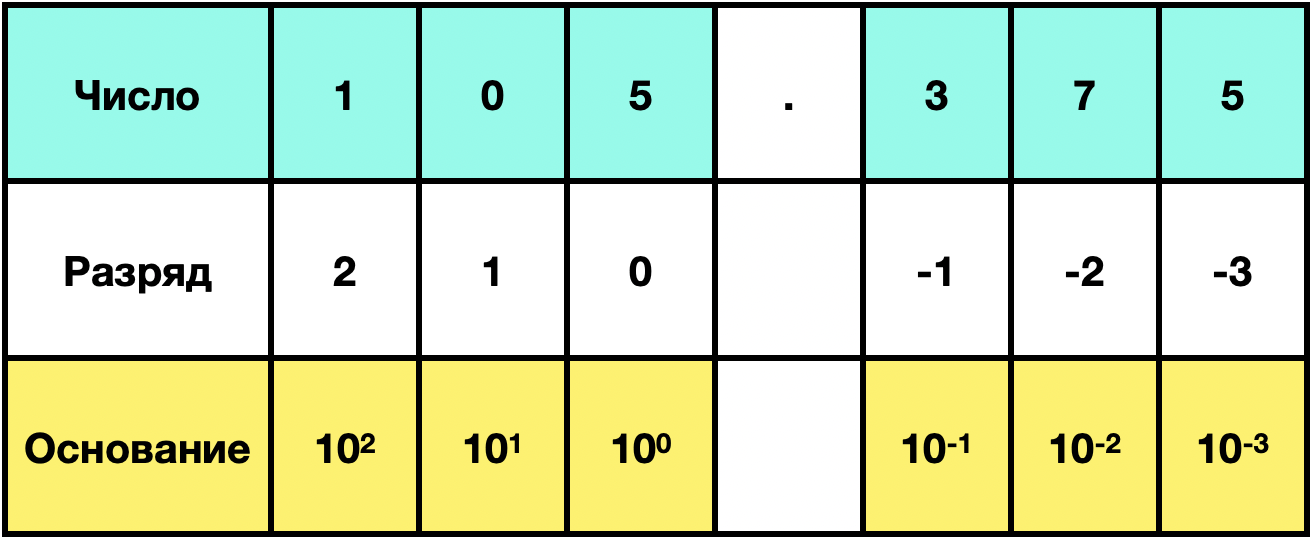
Мы можем видеть, что степень основания у целой части растет от 0 до бесконечности, а у дробной части - от -1 до -бесконечности. Также у нашего числа явно присутствуют целая (105) и дробная (0.375) часть.
Давайте возьмем наше число, разделим его на целую и дробную части, и каждую из них переведем в двоичный вид.
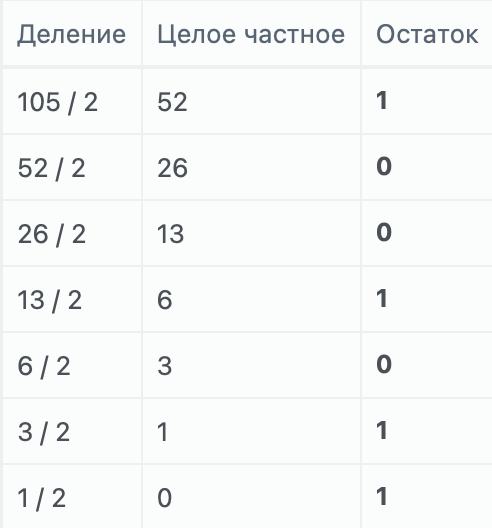
Чтобы перевести целую часть в двоичный вид, нужно ее делить на 2 с остатком, пока результат деления не станет равным нулю. В результате получаем 10510 = 11010012
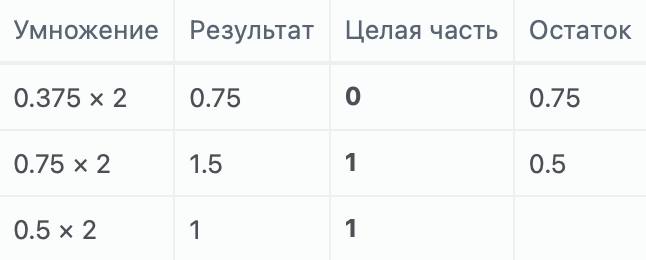
Чтобы перевести дробную часть числа в двоичную систему, необходимо умножать число на основание степени до тех пор, пока целая часть не станет равной 1.0. В данном случае мы переводим число в двоичную систему, поэтому основание будет равно 2. Мы записываем число, полученное в основании, а остаток умножаем снова и снова, пока не получится число 1.0. В итоге получаем 0.37510 = 0.0112
Для лучшего понимания можете попробовать самостоятельно перевести числа из десятичной системы в двоичную и обратно
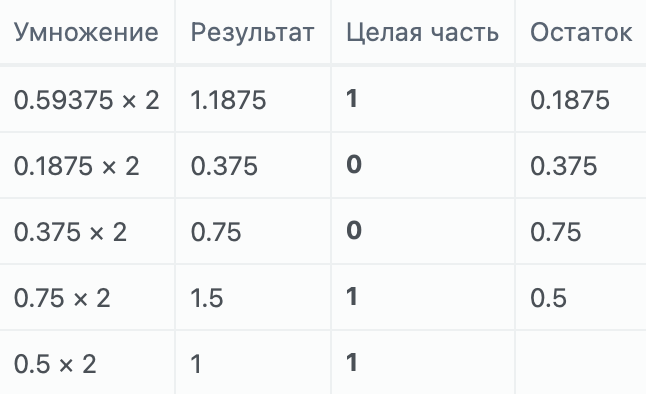
Для примера можем взять число побольше. 0.59375. В двоичном виде это число равно 0.5937510 = 0.100112.
А получили мы это следующим образом:
С этим разобрались, теперь у нас есть понимание того, как математически можно перевести десятичные цифры в двоичные.
Так будет выглядеть число 105.375 в двоичном виде:
Прежде чем продолжить разбираться, как все это хранится в памяти процессора, нужно отметить, что числа, которые мы переводили до этого момента, очень легко поддаются переводу. Однако что будет, если мы попытаемся перевести число 0.9 в двоичную систему?
Давайте попробуем:
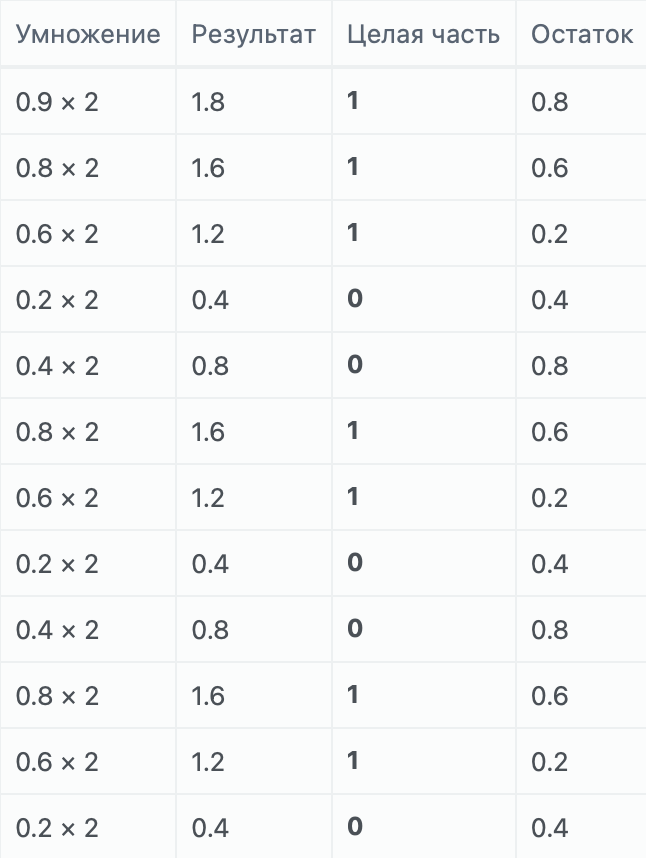
Можно заметить, что в определенный момент результат 0.4 начинает повторяться снова и снова, и мы получаем бесконечный цикл. Из этого следует, что некоторые числа невозможно представить в двоичной системе счисления, так как дробная часть числа при переводе будет бесконечно повторяться. Повторяющуюся дробную часть мы обозначим фигурными скобками, что будет означать. Это называется периодом. 0.910 = 0.11100(1100)2.
Взяв полученное число, давайте попробуем перевести его обратно в десятичный вид. Тут сразу можно заметить, что при переводе числа обратно мы получаем немного отличное от числа 0.9 число. Казалось бы, всего лишь разные системы счисления. Сами цифры в итоге должны быть одинаковые, но почему мы получаем разный ответ при переводе?
0.11100110012 = (0 × 20) + (1 × 2-1) + (1 × 2-2) + (1 × 2-3) + (0 × 2-4) + (0 × 2-5) + (1 × 2-6) + (1 × 2-7) + (0 × 2-8) + (0 × 2-9) + (1 × 2-10) = 0 + 0.5 + 0.25 + 0.125 + 0 + 0 + 0.015625 + 0.0078125 + 0 + 0 + 0.0009765625 = 0.899414062510
Это пример той же математической несовершенности, о которой упоминалось ранее, и с которой нам нужно мириться. Некоторые числа теряют точность, и мы никогда не получим изначальное число из-за того, что часть числа представлена в периоде (а он бесконечный). Из этого следует запомнить одно правило: некоторые дроби, представленные в десятичной системе счисления, невозможно из-за ограничений математики представить в двоичном виде. Именно поэтому при попытке сложить числа 0.1 + 0.2 мы получаем странный результат. Их просто невозможно перевести в двоичный вид, сохраняя точность. Из-за этого результат сложения выглядит не совсем очевидным, так как после перевода чисел из десятичной системы в двоичную и обратно была потеряна точность числа.
Сохранение числа в память компьютера
А теперь давайте перейдем непосредственно к компьютеру. Для сохранения чисел с плавающей точкой процессор компьютера выполняет следующий алгоритм:
Переводит число из десятичной в двоичную систему
Получившиеся число переводит в экспоненциальную запись
Число в экспоненциальной записи поместить в 32 бита (для примера будем брать регистр объемом памяти равный 32 битам).
Для того чтобы понять какие проблемы могут возникнуть, мы попытаемся разобрать этот алгоритм на реальных примерах. Возьмем числа 0.59375, -8.75, 3.9 и попробуем перевести их в двоичный вид.
Начнем с числа -8.75. Переведем целую и дробную участь числа в двоичный вид. В результате мы получим число -8.7510 = -1000.112.
Число 0.5937510 = 0.100112 тоже переводится без особых проблем
А вот число 3.9 перевести в двоичный вид мы не можем, поэтому запишем это число в периоде 3.910 = 11.11100(1100)2.
Так мы выполнили первый этап алгоритма. Перевели числа из десятичного в двоичный вид. Далее попробуем записать эти числа в экспоненциальной записи:
Если попытаться объяснить что такое экспоненциальная запись простым языком не используя такие слова как мантисса и порядок, то я бы описал это так:
При экспоненциальной запись берется произвольное число, каким бы большим или маленьким оно не было, оставляется одна цифра перед точкой, а все остальное записывается как дробная часть в виде степени.
Зачем нам нужна экспоненциальная запись
Если у нас слишком большие или маленькие цифры, например число 10000000000, то его проще записать как 1 * 1010. Экспоненциальной запись позволяет записывать очень длинные цифры в компактном виде. А степень над множителем просто указывает точность.
Далее давайте попробуем привести наши получившиеся числа в двоичной системе в экспоненциальный вид. На примере числа -8.7510 = -1000.112 мы должны сдвинуть точку на 3 разряда влево. Так у нас получится число -1.000112 * 103.
Теперь число 0.5937510 = 0.100112. Тут все тоже самое за исключением того, что точку двигаем в право так как степень положительная. В данном случае мы получим число 1.00112 * 10-1.
И последнее число 3.910 = 11.11100(1100)2 после перевода превращается 1.111100(1100)2 * 101.
Итого у нас получилось 3 числа в следующем виде:
-8.7510 = -1.000112 * 103
0.5937510 = 1.00112 * 10-1
3.910 = 1.111100(1100)2 * 101
Теперь нам остался последний этап алгоритма - записать полученные числа в память. Как нам это сделать? Для примера возьмем объем памяти равным 32 бита.



Первый бит отводится под знак, как и в целых числах. Получается если наше число меньше нуля, то в этот бит будет записана единица, и ноль в обратном случае.
Записав знак в старший бит, у нас остается еще 31 бит для того чтобы записать остаток числа. Для этого, разработчики стандарта IEEE-754 решили, что они выделят 23 бита для хранения дробной части (F - с английского fraction). Однако тут сразу стоит заметить, что в экспоненциональной записи, целая часть нашего числа, которое мы заранее перевели в двоичный вид, всегда равна единице. Соответсвенно в стандарте решили, что нет смысла записывать эту единицу и тратить на нее лишний бит, поэтому при записи числа в память, целую часть, просто опускают. Это позволяет увеличить точность на 1 бит.
Записав всю дробную часть в отведенные 23 бита и опустив единицу, мы получаем следующий вид:



Мы можем видеть, что дробная часть записывается слева направо, а все незанятое пространство заполняется нулями.
С числами 0.59375 и -8.75 все понятно. А как быть с числом 3.9 у которого дробная часть в двоичном виде записывается в периоде который по своей сути бесконечный? На разных машинах поведение может отличаться, но в общем алгоритмм следующий: мы будем записывать значения до тех пор, пока у нас не закончится место, и та дробная часть которая поместилась в отведенные 23 бита и будет означать нашу точность.
Из этого мы можем сделать вывод, что компьютер записывает числа с плавающей точкой с определенной точностью, так как физически невозможно записать число в периоде, который потенциально бесконечный. Однако у нас есть возможность повысить эту точность, увеличив объем выделенной памяти с 32 до 64 бит. В таком случае стандарт выделяет 52 бита для записи дробной части числа.
Теперь нам остался последний шаг: нужно записать степень, которая даст понять, насколько мы сдвинули точку, переводя число в экспоненциальный вид. Для хранения степени ученые решили выделить оставшиеся 8 бит (E - с английского exponent).
Но прежде чем записать оставшуюся часть, давайте еще раз глянем на наши цифры в экспоненциональном виде: -1.000112 * 103 , 1.00112 * 10-1 и 1.111100(1100)2 * 101. Можно заметить, что основание степени всегда равно 10. В первом примере мы имеем 103, во втором 10-1 и в третьем 101. Поэтому так же как с целой частью числа, мы основании степени хранить не будем. Остается только сама степень.

У внимательных читателей мог возникнуть вопрос: "А что делать, если у нас степень со знаком минус? Что делать в таком случае? Будет ли выделен 1 бит из этих 8 бит под знак, как и с целыми числами?”
Давайте попробуем реализовать это решение на примере двух чисел -0.7510 = 1.12 * 10-1 и 410 = 1.02 * 102. В качестве первого бита из 8 выделенных бит будем записывать знак. Тогда мы получим следующее


И тут сразу можно заметить две проблемы. Первая заключается в том, что процессор при сравнении двух чисел будет побитово проходиться по ним и сравнивать значения. Дойдя до числа с отрицательным битом, он увидит там единицу и решит, что это число больше, и операция сравнения будет неправильной.
А вторая проблема заключается в том, что мы выделяем один бит на хранения знака из-за чего наша и точность станет ниже.
Для решения этих проблем ученые придумали очень хитрое решение: диапазон чисел от 0 до 255 был разделен на две части, при этом число посередине (12710 = 011111112) стало восприниматься как 0. Все числа больше 127 воспринимались процессором как положительные, а меньше 127 - как отрицательные. Таким образом, появился диапазон чисел от 0 до 127 с минусом и от 127 до 255 с плюсом, что позволяло записывать числа с точностью до 10127.
Note: Если быть точным, то диапазон положительных был от 0 до 126, а для отрицательных от 0 до -127 но об этом позже.
Для наглядности возьмем те же 2 числа, -0.7510 = 1.12 * 10-1 и 410 = 1.02 * 102. Теперь по формуле степень сдвига точки будет записана следующим образом:


Теперь когда процессор попытается сохранить число, он сделает следующее: возьмет 12710 = 011111112 и добавит к нему число степени в двоичном виде. И теперь при попытке сравнить эти 2 числа, процессор будет выдавать результаты корректно. Наши числа сохранены в памяти таким образом, что процессору легче их сравнивать и память расходуется более экономно.
Вернемся к нашим числам. После применения последнего шага алгоритма, наши числа будут выглядеть следующим образом:



Специальные значения
При работе с числами с плавающей точкой возможно столкновение со специальными значениями, которые могут быть представлены только определенными комбинациями битов. Некоторые из таких значений - NaN (Not a Number) и +-Infinity.
Для отображения этих специальных значений в устройствах с плавающей точкой ученые решили использовать пару комбинаций битов в экспоненте. Для того чтобы отобразить значение Inf, экспонента должна содержать только единицы, а дробная часть должна быть равна нулю. Отрицательное или положительное бесконечное значение зависит от старшего бита знака.


Также стоит упомянуть NaN (Not a Number), который используется для обозначения несуществующего числа. Например, если мы пытаемся получить корень из отрицательного числа, в данном случае в экспоненту также будут записаны все единицы, а вот знаковый бит и биты дробной части могут иметь произвольные значения.

По причинам описанные выше, положительная степень числа может храниться от 127-254 значений, потому что 25510 = 111111112 занято под специальное значение.
Заключение
В этой статье мы рассмотрели основные проблемы перевода чисел из десятичной в двоичную систему, принципы работы компьютера с числами с плавающей точкой, а также возможные проблемы и способы их решения, на которые обращают внимание программисты.
В продолжение к чтению, если вдруг интересно почитать как компьютер работает с Unicode простым языком, вот отличная статья на эту тему.