greck Dec 20 2023 at 23:15

3. Information theory and ML. Forecast

31 min

523

Mathematics*Machine learning*

Translation

Original author: greck

Part 1 - Entropy

Part 2 - Mutual Information

In this third part, we will discuss Machine Learning, specifically the prediction task in the context of information theory.

The concept of Mutual Information (MI) is related to the prediction task. In fact, the prediction task can be viewed as the problem of extracting information about the signal from the factors. Some part of the information about the signal is contained in the factors. If you write a function that calculates a value close to the signal based on the factors, then this will demonstrate that you have been able to extract MI between the signal and the factors.

What is Machine Learning?

To move forward, we need fundamental concepts from Machine Learning (ML), such as factors, target, loss function, training and test sets, overfitting and underfitting and their variations, regularization, and different types of data leakage.

Factors (features) are what you input, and the signal (target) is what you need to predict using the features. For example, if you need to forecast the temperature tomorrow at 12:00 in a specific city, that's the target, while you are given a set of numbers about today and previous days: temperature, pressure, humidity, wind direction, and wind speed in this and neighboring cities at different times of the day – these are the features.

Training Data is a set of examples (also known as samples) with known correct answers, meaning rows in a table that contain both the feature fields (features = (f1, f2, ..., fn)) and the target field. Data is commonly divided into two parts – the training set and the test set. It looks something like this:

Training set:

id	f₁	f₂	...	*target*	*predict*
1	1.234	3.678	...	1.23	?
2	2.345	6.123	...	2.34	?
...	...	...	...	...	...
18987	1.432	3.444	....	5.67	?

Test set:

id	f₁	f₂	...	*target*	*predict*
18988	6.321	6.545	...	4.987	?
18989	4.123	2.348	...	3.765	?
...	...	...	...	....	...
30756	2.678	3.187	...	2.593	?

In broad terms, the prediction task can be formulated in a Kaggle-style competition:

Prediction Task (ML Task): You are given a training set. Implement a function $\mathcal{P}(f_1, \ldots, f_k)$ in code that, based on the given features, returns a value as close as possible to the target. The measure of closeness is defined by a loss function, and the value of this function is called the prediction error: , where $predict = \mathcal{P}(f_1, \ldots, f_k)$ . The quality of the prediction is determined by the average error during the application of this prediction in real-life scenarios, but in practice, a test set hidden from you is used to evaluate this average error.

The quantity $\xi = predict - target$ has a special name - the residual. Two popular variants of loss functions for predicting real values are:

Mean Squared Error (MSE) - also known as the average squared residual.
Mean Absolute Error (MAE) - also known as the L1 error.

In practice, the ML task is more general and high-level. Specifically, you need to develop a moderately universal ML model - a way to get functions $\mathcal{P}(f_1, \ldots, f_n)$ from a given training set and a specified loss function. You also need to perform model evaluation: monitor the prediction quality in a working system, be able to update trained models (step by step, creating new versions, or modifying the model's internal weights in an online mode), improve the model's quality, and control the cleanliness and quality of the features.

The process of getting the function $\mathcal{P}(f_1, \ldots, f_n)$ from the training set is called training. Popular classes of ML models include:

Linear Model: In a linear model, where $\mathcal{P}(f_1, \ldots, f_n) = \sum_{i} w_i \cdot f_i$ , the training process typically involves parameter tuning , usually done through gradient descent.
Gradient Boosted Trees (GBT): GBT is a model where the function looks like a sum of multiple terms (hundreds or thousands), with each term being a decision tree. In the nodes of these trees, there are conditions based on the features, and in the leaves, specific numbers are assigned. Each term can be thought of as a system of nested if-conditions on feature values, with simple numbers in the final leaves. GBT is not just about the solution being a sum of trees but also a specific algorithm for getting these terms. There are many ready-made programs for training GBT, such as CatBoost and xgboost.
Neural Networks: In its simplest basic form, a neural network model appears as $\mathcal{P}(\vec{f}) = W_k\odot W_{k-1}\odot \ldots W_1 \odot \vec{f}$ , , where are matrices, and their sizes are determined by the model developer. The features are represented as a vector $\vec{f} = |f_1, \ldots, f_n|^{T}$ , and the operator $\odot$ represents element-wise multiplication of a vector by a matrix followed by setting all negative values in the resulting vector to zero. Operators are applied from right to left, which is important in the case of this zeroing. The matrices are referred to as layers of the neural network, and the number of matrices determines the depth of the network. Instead of zeroing negatives, various other non-linear transformations can be applied. Without non-linear transformations after the matrix multiplication, all matrices could be collapsed into one, and the space of possible functions would not differ from what a linear model defines. I described a linear architecture for a neural network, but more complex architectures are possible. For instance:
$\mathcal{P}(\vec{f})=W_6\odot(W_1\odot W_2 \cdot \vec{f} + W_3\odot W_4 \odot W_5\odot W_2\odot \vec{f})+W_7\odot \vec{f}$ .
In addition to various element-wise non-linear transformations and matrix multiplications, neural networks can use operators for scalar vector products and element-wise maximum operations for two vectors of the same dimension, combining vectors into a longer one, and more. You can think of a general architecture for the prediction function, where a vector is input, and then the response is constructed using operators $\{+, -, \cdot, \max \}$ , non-linear functions $\{\tanh, \mathrm{abs}, \max(0, \cdot), \ldots\}$ , and weights $\{w_1, w_2, \ldots\}$ . In this sense, neural networks can represent functions of quite a general form. In reality, the architecture of the function $\mathcal{P}$ is called a neural network when it contains something resembling a chain like $W_k\odot W_{k-1}\odot \ldots W_1 \odot \vec{f}$ . Essentially, we have a regression problem - to adjust parameters (weights) in a parametrically defined function to minimize the error. There are numerous methods for training neural networks, most of which are iterative, and the module responsible for weight updates is what programmers refer to as an optimizer, such as AdamOptimizer, for example.

ML Terminology

In regression analysis, many important terms have emerged, allowing for a better understanding of the content of prediction tasks and avoiding common mistakes. These terms have been carried over into Machine Learning (ML) with little to no modification. Here, I will present the fundamental concepts, aiming to highlight their connections to information theory.

Overfitting

Overfitting (retraining) occurs when the model you have selected is more complex than the actual reality underlying the target, and/or when there is insufficient data to support training such a complex model. There are two main causes of overfitting:

too complex model: The model's structure is significantly more intricate than the reality or does not align with the complexity of the reality it's intended to represent. It's easier to illustrate this with a one-factor model.
Let's say you have 11 data points in your training set , and your model is a 10th-degree polynomial. You can adjust the coefficients in the polynomial in such a way that it "touches" every data point in the training set, but this doesn't guarantee good predictive performance.
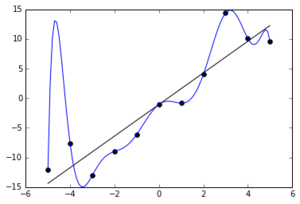
The blue line is a 10th-degree polynomial
that was able to precisely replicate the training set of 11 points.
However, the correct model is likely more linear (the black line), and the deviations from it are either noise or something explained by factors that we don't have.

A polynomial of the 10th degree is an obvious and frequently used example of overfitting. Polynomials of low degrees with many variables can also lead to overfitting. For instance, you can choose a model like predict = a 3rd-degree polynomial of 100 factors (by the way, how many coefficients does it have?), while in reality, the prediction corresponds to a 2nd-degree polynomial of the factors plus random noise. If you have a sufficient amount of data, classical regression methods can yield an acceptable result, and the coefficients for the 3rd-degree terms will be very small. These 3rd-degree terms will make a small contribution to the prediction for typical factor values (as in the case of interpolation). However, in the extreme values of the factors, where the prediction is more of an extrapolation than interpolation, the high-degree terms will have a noticeable impact and degrade the prediction quality. Moreover, when you have limited data, noise might be mistaken for true information, causing the prediction to try to fit every point in the training data.

Insufficient training data: Your model may roughly match reality, but you might not have enough training data. Let's use the polynomial example again: suppose both reality and your model are 3rd-degree polynomials of two factors. This polynomial is defined by 10 coefficients, meaning the space of possible predictors is 10-dimensional. If you have 9 examples in your training pool, writing the equation "polynomial(features_i) = target_i" for each example will give you 9 equations for these coefficients, which is insufficient to uniquely determine the 10 coefficients. In the space of possible predictors, you will get a line, and each point on this line represents a predictor that perfectly replicates what you have in your training pool. You can randomly choose one of them, and there is a high probability that it will be a poor predictor.
Important note about training multi-parameter models. The above example may seem artificial, but the truth is that modern neural network models can contain millions of parameters or even more. For instance, the GPT-3 language model contains 175 billion parameters.

If your model has N = 175 billion parameters, and the size of the training pool is M = 1 billion, you essentially have an infinite set of models that perfectly fit the training data, and this set is essentially a manifold of dimension N - M = 174 billion.

In the case of deep multi-parameter neural networks, the "insufficient train data" effect becomes highly pronounced if handled incorrectly. Specifically, seeking the strict minimum of the error on the training pool results in a poor, overfitted predictor. This is not how things are done in practice. Various techniques and intuitions have been developed for training a model with N parameters on M examples, where M is significantly smaller than N. Regularization terms are added to the loss function (L2, L1), Stochastic Gradient Descent, Dropout Layers, Early Stopping, pruning, and other techniques are used.
IMPORTANT: Understanding these techniques and knowing how to apply them largely defines expertise in machine learning.

Underfitting

Underfitting occurs when the prediction model is simpler than reality. Just like in the case of overfitting, there are two main reasons for underfitting:

too simplistic model: Choosing a model that is too simple and overly simplifies what is behind the target in reality. These cases are still encountered in production, and they are usually linear models. Linear models are appealing due to their simplicity and the presence of mathematical theorems that justify and describe their predictive abilities. However, it can be stated with confidence that if you decide to use linear models to predict currency exchange rates, weather, purchase probabilities, or credit repayment probabilities, you will get under-fitted weak model.
too early stopping: Training processes for models are typically iterative. If too few iterations are performed, an undertrained model results.

Data leakage

Data leakage is when, during training, you used information that exists in the test pool or data that is not available or differs from what will be available in practice when applying the model in real-life situations. Models that can take advantage of this leakage will have unreasonably low errors on the test pool and may be selected for real-world use. There are several types of data leakage:

Target leakage into factors: If, in a temperature prediction task, you add a factor - the average temperature for the past K days, and during training, some of the K days include the target day for which the prediction should be made, then you will get a flawed or non-functional predictor. More complex leaks can occur through features. In the case of predicting some future event, you must repeatedly ensure that when calculating features for the training pool, data got during or after that event is not used.
Simple test pool leakage: Sometimes it's straightforward - rows from the test pool end up in the training pool.
Leakage through hyperparameter tuning: The rule that only the training pool should be used for training is deceptively simple. It's easy to be misled here. A typical example of implicit leakage is hyperparameter tuning during training. Every training algorithm has hyperparameters. For instance, in gradient descent, there are parameters like "learning rate" and a parameter defining the stopping criterion. Moreover, you can add regularization components to the Loss function, like $R_2=\lambda_2 \sum w_i^2$ and $R_1=\lambda_1 \sum |w_i|$ , and now you have two more hyperparameters $\lambda_1$ and $\lambda_2$ . The prefix 'hyper' is used to differentiate internal model parameters (weights) from parameters influencing the training process.
So, suppose you decide to iterate through different training hyperparameters and select those hyperparameters that minimize the error on the test set. It's important to understand that there's a leakage of the test set into the model happening here. The 'trap' hidden here is easy to understand from the standpoint of information theory. When you ask what the error is on the test set, you're extracting information about that test set. Then, when you make decisions based on this information that ultimately affect the weights of your model, bits of this information end up in the model's weights.
One can further illustrate the concept of test set leakage by pushing the notion of hyperparameters to the absurd. After all, the distinction between weights (parameters) and hyperparameters (training process parameters) is purely formal. Let's name all the model weights, such as the coefficients of a 10-degree polynomial, as hyperparameters, and we'll have no training process (the set of internal weights will be empty). Then, let's embark on an insane loop to search through all possible combinations of hyperparameter values (each parameter ranging from -1000 to +1000 with a step of $10^{-6}$ and compute the error on the test set. Clearly, after billions of years, we'll find such a combination of parameters that yields a very small error on the test set, and we could repost the same image above, but with a different captio:
The blue line represents a polynomial of the 10th degree that managed to perfectly replicate the test pool of 11 points.

This predictor will perform well on the test pool but poorly in real life.

In practice, models with thousands or millions of weights are used, and these effects are noticeable in larger datasets, especially with data leakage from the future (see below).
It's important to understand that test leakage through hyperparameter tuning always happens one way or another. Even if you've created a separate validation pool for tuning hyperparameters and haven't used the test pool for that purpose, there's still a moment when you compute the quality metric on the test pool. Later on, when you have several models evaluated on the test pool, choosing the best model based on the test metric is also considered a form of leakage. However, not all such instances of leakage need to be feared.
An important note is when to be concerned about this kind of leakage. If the effective complexity of your model (see the definition below) involves hundreds or more bits, you may not need to fear this type of leakage or allocate a special pool for hyperparameter tuning— the logarithm of the number of attempts for hyperparameter tuning should be noticeably smaller than the complexity of the model.

Data leakage from the future: For instance, when training predictors for click-through rates on ads, ideally, the training pool should contain data exclusively available before a specific date, let's say date X, which is the minimum date of events in the test pool. Otherwise, sneaky leaks like the following could occur. Suppose we have a set of ad display events labeled with target = 1 for clicked events and target = 0 for non-clicked ones. And let's assume we split this event set into the training and test pools not based on the date boundary X but randomly, for instance, in a 50:50 ratio. It's known that users tend to click on several ads of the same topic in a row within a few minutes, selecting the desired product or service. Consequently, these sequences of multiple clicks might randomly split between the training and test pools. You can artificially create a model with a leak: take the best correct model without a leak and additionally memorize the facts "user U clicked on topic T" from the training log. Then, while using the model, slightly increase the click probability for cases (U, T) from this set. This will improve the model in terms of the test pool error but worsen its practical application on new data. We've described an artificial model, yet it's easy to imagine a natural mechanism for memorizing (U, T) pairs and inflating their probabilities in neural networks and other popular ML algorithms. The presence of such leaks from the future exacerbates the issue of leakage through hyperparameters. Models overtuned towards memorizing data will win on such a test pool with leakage. To describe this problem more broadly: a model can overfit to the test set if the mutual information between an example in the train set and an example in the test set is greater than that between an example in the train set and a real example when using the model in real life.

Tasks

Task 3.1 Let the reality be such that $target = w_0 + w_1\cdot f + w_2\cdot f^2+ \nu,$ where $\nu$ – is a random number from $\mathcal{N}(0,\alpha^2),$ $\alpha=0.2.$ The factor is sampled from $\mathcal{N}(0,1).$ On average, how many training data points are needed to get weight estimates that are equal to the true weights within a mean square error of $\varepsilon=0.01$ , given an appropriate model for reality?
Consider that the prior distribution of weights is a normal distribution $\mathcal{N}(0,\sigma^2).$ Express the answer as a function of $\alpha$ , $\varepsilon$ , $\sigma.$ How does the prediction error depend on the size of the training dataset?

Answer

There's a method to get an answer "from physicists." Let the size of the training dataset be . From problem 1.16, we have the intuition that $\varepsilon = c / \sqrt{n}$ . The constant in this problem is a function of $\alpha$ and $\sigma$ . But is there a dependency of on $\sigma$ ? In fact, there isn't. Indeed, the noise $\alpha\cdot \nu$ erases digits in the decimal representation of the value, starting at some point after the decimal. When $\sigma$ increases, more significant digits remain, and that's exactly how much more we learn about the coefficients $\{w_0, w_1, w_2\}.$ Thus, with an increase in $\sigma$ , the position in the decimal representation of $\{w_0, w_1, w_2\}$ , from which there is uncertainty, remains the same. Due to $\sigma$ not being involved in the formula and considering dimensional considerations, the formula should look like this:

$\varepsilon =c_0 \cdot {\alpha \over \sqrt{n}}$

Where the empirically computed constant is approximately equal to 0.9. Consequently, we get the answer $n = 0.8\cdot \left({\alpha \over \varepsilon} \right)^2$ .

The error of thevalue itself equals:

$mse=\sqrt{\varepsilon^2 + \alpha^2}=\alpha \cdot \sqrt{1+0.8/n}$

This is a consequence of adding two independent random variables $w'_0 + w'_1\cdot f + w'_2\cdot f^2$ and $\nu$ their variances add up. They should be independent in the correct forecast because if they are dependent, the model can be improved by calibrating the forecast in some way.

Thus, in this prediction problem and many practical situations, there's an unavoidable error $\alpha$ . It determines two things:
(1) the error you'll get for a very large training set (as $n\to \infty$ , we have $mse=\alpha \sqrt{1 + \beta /n}\to \alpha$ )
(2) the size of the set necessary to achieve a certain specified error in internal parameters, which quadratically depends on this unavoidable error: $n=\beta \cdot (\alpha/\varepsilon)^2$

The unavoidable error $\alpha$ is defined by the amount of information in the signal that is fundamentally absent in your factors. The size of the training set required to get a model of a certain accuracy mse, quadratically depends on this error:

$n={\beta \over (mse/\alpha)^2 -1 }\approx \beta \cdot (\alpha / mse)^2 \; \;\mathrm{при\;маленьких} \; \alpha/mse$

Someone might have the slightly incorrect intuition that reducing this error is crucial and that adding factors where new information about the signal might be hidden is an extremely beneficial move. Sometimes that's true. However, in reality, having more factors means having more internal weights, and you need more information to figure out the first significant digits of those weights. Increasing model complexity by adding new factors sometimes nullifies the beneficial effect of new information if you don't increase the size of the training set (i.e., increase the number of rows in the training pool), especially when the new factors are less informative than the existing ones.

Moreover, factors are often dependent and inherently contain a noisy component. Assessing the utility of new factors and conducting factor selection is a separate and complex topic on its own.

Task 3.2. Let reality be such that the target is a second-degree polynomial of 10 factors, where the coefficients in the polynomial are numbers sampled once from $\mathcal{N}(0,1),$ and the factors are independent random numbers from $\mathcal{N}(0,1)$ . How much data is needed in the training set to achieve acceptable prediction quality when all factors lie in the range [-1, 1], assuming the model is correct, meaning it is a second-degree polynomial?
And what if the model is a third-degree polynomial?

Task 3.3. Build a model of users who tend to click more on ads of a particular theme at any given time and ensure that dividing the dataset into a training and test set randomly, rather than by time, leads to data leakage from the future.
You can take, for instance, this model: each user has 10 favorite themes, which we know and store in the user's profile. User activity is divided into sessions, each lasting 5 minutes, during which the user sees exactly 10 ads from one of their 10 themes, randomly chosen from their favorites. In each session, the user is particularly interested in one of these 10 themes, and there are no factors allowing us to guess which one specifically. The probability of clicking for this "hot" theme is twice as high as usual. Based on each user's click history, we know the click probabilities for their 10 themes well, and if ordered by interest for a specific user, the vector of these probabilities is {0.10, 0.11, 0.12, ..., 0.19}. The user ID and the category number are the available factors. How much can the likelihood of predicting the click probability on the test set increase if we assume that each session was equally divided between the training and test sets (5 events went into one pool and 5 into the other), and the statistics from 5 events in the training set can be used to predict the click probability for 5 others?
It is suggested to experimentally achieve overfitting due to data leakage from the future by using some ML program like CatBoost.

Definition 3.1. The implementation $\varepsilon$ - complexity of a function ( $\varepsilon$ - IC) is the amount of information about the function that needs to be communicated from one programmer to another, enabling the latter to reproduce it with a mean squared error not exceeding $\varepsilon$ . Two programmers agree in advance on a parametric family of functions and the prior distribution of parameters (weights) within this family.
The effective complexity of a model is the minimum implementation complexity of a function among all possible functions that provide the same predictive quality as the given model.

Task 3.4. What is the average $\varepsilon$ - IC of a function of the form

$p(f_1,\ldots,f_n)=\sum_{i=1}^n w_i\cdot f_i$

of n factors, where the weights are sampled from the distribution $\mathcal{N}(0,\sigma^2)$ , and the factors are sampled from $\mathcal{N}(0,1)$ ?

Answer

When the factors are fixed, the function's error is determined by the errors in the weights using the formula:

$\delta p^2 = \sum_i \delta w_i ^2 f_i^2$

On average, considering all possible factor values, we get $\delta p^2 = {\sum}_i \delta w_i ^2$ . If we desire $\delta p^2 \le \varepsilon^2$ , then the weights need to be transmitted with precision $\delta w_i \le \varepsilon^2 /n$ .

Hence, according to the answer in task 1.9, on average, it will be necessary to transmit $n\cdot \log(\sqrt{n}\cdot \sigma/\varepsilon)$ bits. Here lies an important property of very complex models – determining the complexity of a complex model isn't as reliant on the quality or precision of prior knowledge about the weights or the achieved accuracy. The primary component in the IC of the model is $0.5 \cdot n\cdot \log n$ , where n represents some effective number of weights contributing equally and beneficially to the model.

Task 3.5. The function t(id) is defined by a table as a function of a single factor – the category ID. There are N = 1 million categories with varying proportions in the data, which can be considered as proportions got by sampling 1 million numbers from an exponential distribution, followed by normalization to ensure their sum equals 1 (this sampling corresponds to sampling once from a Dirichlet distribution with parameters {1,1,...,1} – 1 million ones). The values of the function t for these categories are sampled independently from a beta distribution $B(\alpha, \beta),$
where $\alpha=2,$ and $\beta=10$ .

What is the average $\varepsilon$ - IC of such a function?

Answer

First, let's describe the behavior of this function for very small $\varepsilon$ . When $\varepsilon \ll 1/10^6$ , we are forced to store a table function – 1 million values. It's possible to numerically or through the formula from Wikipedia calculate the entropy of the beta distribution $B(\alpha, \beta)$ . Next, assume that we want to convey to another programmer that the value t for a specific category i lies around some fixed value with an allowed error of $\varepsilon$ . This is equivalent to narrowing the "hat" of the distribution $B(\alpha, \beta)$ to, let's say, a normal distribution $\mathcal{N}(t_i, \varepsilon^2).$ The difference in entropy between $B(\alpha, \beta)$ and $\mathcal{N}(t_i, \varepsilon^2)$ is approximately $-2.38 -\log \varepsilon$ . This needs to be done for 1 million categories, so for very small $\varepsilon$ , the answer is $N\cdot (-2.38 + \log 1/\varepsilon)$ .

For larger $\varepsilon$ (but still noticeably less than 1), another strategy works. Let's divide the interval [0,1] into equal segments of length $\delta$ , and for each category, transmit the number of the segment in which the function value for this category falls. This information has a volume of $N\cdot (H_{B(2,10)}+ \log(1/\delta))$ (see task 1.7). As a result, in each answer, our error will be limited by the length of the segment in which we landed. If we consider the midpoint of the segment as the answer and assume uniformity of the distribution (which is acceptable when the segments are small), then the error within a segment of length $\delta$ is $\delta/\sqrt{12}$ . Therefore, to get the specified average error $\varepsilon$ , the segments should be of length $\delta=\sqrt{12}\cdot \varepsilon$ . Hence, the overall answer is $N\cdot (-2.20487 + \log 1/\varepsilon)$ .

Both approaches yield an answer of the form $N\cdot (c + \log 1/\varepsilon)$ . The idea of using the Bloom filter to store sets of categories for each segment also provides the same result.

Task 3.6. Let's say in the previous task, the function represents the probability of clicking on an advertisement. Let's renumber all the categories in descending order of their true proportions and denote the ordinal number as order_id, while the original random identifier is denoted as id. We propose considering different machine learning options by coarsening the number (identifier) of the category to a natural number from 1 to 1000. This limitation might be related, for instance, to the need to store statistics on historical data, where you only have the capability to store 1000 pairs (displays, clicks). The options for coarsening the category identifier are:
(a) Coarsened identifier equals id' = id // 1000 (integer division by 1000);
(b) Coarsened identifier equals id' = order_id for the top 999 categories by proportion, while assigning identifier 1000 to all the others;
(c) Some other method of coarsening id' = G(id), where G is a deterministic function that you can construct based on click statistics from 100 million displays, where each display has a category with an equal probability of categories, and clicks occur based on the click probability for that category.
Evaluate the error value in these three approaches, where and $LL=-{\sum}_{i=1}^n t_i \log(p_i) + (1-t_i)\log(1-p_i)$ , and is the value for a perfect forecast where .

Task 3.7. Let reality be such that $target ={\sum}_{i=1}^{45} w_i\cdot f_i +0.02 \cdot \nu$ , where $\nu$ is noise,

a random number from $\mathcal{N}(0,1)$ . And your model $predict = {\sum}_{i=1}^{50} w_i\cdot f_i +0.02 \cdot \nu,$ where the weights $w_1,w_2, \ldots,w_{70}$ are unknown to you and have a Laplace prior distribution with a mean of 0 and variance of 1. The last 5 factors of the model are effectively useless for prediction. What should be the size of the training pool to achieve a mean squared prediction error where

$mse={\sum}_{i=1}^n(predict_i - target_i)^2 / n \le 0.04^2$ .

Generate three pools: №1, №2, №3 with sizes 50, 50, 100000 and find out which action is better - (a), (b), or (c):
(a) Merge two pools into one and based on the combined pool, find the best weights minimizing the on this pool.
(b) For different pairs $(\lambda_1, \lambda_2)$ , find the best weights minimizing $mse + \lambda_1 \sum |w_i| + \lambda_2 \cdot \sum w_i^2$ on pool №1; from all pairs, choose $\lambda_1$ , $\lambda_2$ that minimizes on pool №2; suggested pairs $(\lambda_1, \lambda_2)$ should be taken from sets $A \times B,$ where and are geometric progressions with from to 1. Draw a plot of the error as a function of $\lambda_1$ with $\lambda_2 = 0$ .
(c) Merge two pools into one and based on the combined pool, find the best weights minimizing $mse + \lambda_1 \sum |w_i| + \lambda_2 \cdot \sum w_i^2$ on this pool; take the values of $\lambda_1$ , $\lambda_2$ from step (b).

The method is better the smaller the error on pool №3, which corresponds to the model's application in reality. Is the winner stable when generating new pools? Draw a 3x3 table of mse errors on the three pools using these three methods. How does the error on pool №3 decrease with the increase in sizes of pools №1 and №2?

Task 3.8. Let reality be defined by $target =l_1(\vec{f})+ l_2(\vec{f}) +l_3(\vec{f})+\nu$ , where

$\nu$ is noise, a random namber from $\mathcal{N}(0,\delta^2)$ , $\delta=0.02$ .
The factors $\vec{f}=\|f_1,\ldots,f_{m}\|^t$ are independent random variables with a uniform distribution on the interval , .
$l_1(\vec{f})=w_0+\sum w_{i}\cdot f_i$ is a linear function with coefficients from $\mathcal{N}(0,1)$ .
$l_2(\vec{f})={1 \over 2}\sum w_{ij}\cdot f_i\cdot f_j$ is a quadratic homogeneous function where most coefficients $w_{ij}$ are zero, except for randomcoefficients generated from $\mathcal{N}(0,1)$ .
$l_3(\vec{f})={1 \over 6}\sum w_{ijk}\cdot f_i\cdot f_j\cdot f_j$ is a cubic homogeneous function where most coefficients $w_{ijk}$ are zero, except for random coefficients generated from $\mathcal{N}(0,1)$ .

What will be the mean squared error (mse) of prediction on sufficiently large test and training pools for different variations of the $target(\vec{f})$ function (that is, for different samplings of coefficients $w_i, \; w_{ij},\; w_{ijk}$ ) in the case when your model is:

(a0) $\mathcal{P}(\vec{f})=l_1(\vec{f})$ with true coefficient values.
(b0) $\mathcal{P}(\vec{f})=l_1(\vec{f})+l_2(\vec{f})$ with true coefficient values.
(c0) $\mathcal{P}(\vec{f})=l_1(\vec{f})+l_2(\vec{f})+l_3(\vec{f})$ with true coefficient values.
(a1) $\mathcal{P}(\vec{f})=l_1(\vec{f})$ with training (i.e., coefficients got by regression).
(b1) $\mathcal{P}(\vec{f})=l_1(\vec{f})+l_2(\vec{f})$ with training, without knowing which coefficients are zero.
(c1) $\mathcal{P}(\vec{f})=l_1(\vec{f})+l_2(\vec{f})+l_3(\vec{f})$ with training, without knowing which coefficients are zero.
(c2) $\mathcal{P}(\vec{f})=l_1(\vec{f})+l_2(\vec{f})+l_3(\vec{f})$ with training, knowing which coefficients are zero.
(d1) $\mathcal{P}(\vec{f})$ is a neural network with a depth of d = 5 and internal layer size h=5 (internal matrices have a size of h x h).

A sufficiently large training pool is one where doubling it doesn't notably reduce the error on the test set.

A sufficiently large test pool is one where its finite size doesn't introduce an error comparable to the model's error. In other words, a sufficiently large test pool won't allow critical ranking errors among models. The discriminative capacity of the test pool is the difference in model qualities that the test pool confidently allows you to assess. In our task, it's crucial to correctly rank the listed 6 models.

Observe overfitting in these models (except the first two) by reducing the size of the training pool to a certain value for each model. Try to mitigate overfitting by:

Adding regularization terms to the Loss function: $R_1=\lambda_1\cdot \sum |w|,$ $R_2=\lambda_2 \cdot \sum w^2$ ;
Using early stopping.
Employing SGD (Stochastic Gradient Descent).
Modifying the architecture of the neural network.
Adding Dropout.
A combination of these methods.

It's also interesting in this task to study how the degree of overfitting increases and the model's quality decreases with the increase in the number of (extra) parameters. For model (c1), initially, you can consider only those coefficients that are actually non-zero. Then, explore several options by adding some randomly selected extra coefficients to the model. Plot the model's error growth against the logarithm of the number of coefficients in the model. Additionally, create a graph illustrating the change in error for the neural network model (d1) as a function of the number of internal layers and their sizes.

Task 3.9. Let reality be defined as:

$target =w_0+\sum_{i=1}^{m} w_i\cdot f_i+\nu,$

Where:

The weights are sampled from $\mathcal{N}(0,\sigma^2)$ ;
$\nu$ is noise, a random number from $\mathcal{N}(0,\delta^2)$ , $\delta=0.5$ .
The values $f_1,\ldots,f_{m}$ are independent random variables with a normal distribution $\mathcal{N}(0,1)$ ;

How does the error in determining the weights depend on the size of the training data and $m, \; \delta?$

Answer

In the first approximation, the answer is

$mse(w_i) = {\delta \over \sqrt{n}}.\;\;\;\;\;(1)$

And this is a good approximation for the case where $n \gg m$ (when is significantly larger than ).

For n = 0, the best estimate of weights is 0, and the error of this estimation is 1. This error slowly decreases as n increases up to the number m. Then, the error drops significantly faster and as n increases, it approaches the asymptote (1). Through numerical experiments, you can get a graph:

Average squared error of weights, normalized by δ^2 for m=50. The X-axis is normalized by m, meaning X=1 corresponds to n = m. The red line corresponds to the function 1/n. — Average squared error of weights, normalized by δ^2 for m=50.
The X-axis is normalized by m, meaning X=1 corresponds to n = m.
The red line corresponds to the function 1/n.

If anyone has a good analytical approximation for the vicinity of n ~ m, feel free to send it via private message.

Task 3.10. Let reality be defined as:

$target =\sum_{i=1}^{11} w_i\cdot g_i+\nu,$

Where:

The weights are sampled from $\mathcal{N}(0,1)$ ;
$\nu$ is noise, a random number from $\mathcal{N}(0,\delta^2)$ , $\delta=0.5$ .
The values $g_1,\ldots,g_{m}$ are independent random variables with a normal distribution $\mathcal{N}(0,1)$ ;
You are given factors with noise: $f_i = g_i + \zeta_i$ , where the random noise $\zeta_i$ in each example is sampled from $\mathcal{N}(0, z_i^2)$ (represented as $\zeta_i\sim\mathcal{N}(0,z_i^2)),$ and the noise sizes are known and equal to $z_i=0.01 \cdot 2^i$ .

What will be the best forecast if you know the exact values of weights How can you best implement learning in this task (when the weights are unknown and need to be "learned")?

Answer

Let's consider a specific problem regarding adding a new factor to an existing forecast . Suppose:

$target = F_0 + w_1\cdot g_1 + \nu_1,\; \\ \nu_1 \sim \mathcal{N}(0, \delta_1^2), \; g_1\sim \mathcal{N}(0,1), \\ predict_0 = F_0, \\ f_1 = g_1 + \zeta_1, \; \; \zeta_1\sim \mathcal{N}(0,z_1^2)$

Can we reduce the mean squared error (mse) by taking a new forecast:

$predict_1 = predict_0 + w_1\cdot f_1?$

The current error is equal to the variance $D(target - predict_0) = w_1^2 + \delta_1^2.$ The error of the new forecast will be $D(target - predict_1) = w_1^2 \cdot z_1^2+\delta_1^2,$ which is smaller than the old error if

Let's construct a sequence of forecast improvements:

$predict_0 = 0,\\ predict_1 = predict_0 + t_1 \cdot w_1 \cdot f_1, \\ predict_2=predict_1 + t_2\cdot w_2\cdot f_2, \\ \ldots \\ predict_{m} = predict_{m-1} + t_{m}\cdot w_{m}\cdot f_{m}$

The numbers are equal to 0 or 1 – these are indicators of whether we include the factor in the linear forecast or not. $D(target - predict_0) = \sigma_0^2 = w_1^2 + \delta_1^2$ , where

$\delta_1^2 = \sum_{i=2}^{m} w_i^2 + \delta^2$

Then, if we take the first factor, the error will be:

$D(target - predict_1) =\sigma_1^2= w_1\cdot z_1^2 + \delta_1^2$

It's logical to include a new factor in the linear forecast when

Ultimately, the error of the final forecast is:

$D(target - predict_{m}) = \sigma_m^2=\sum_{i=1}^m \min(1, z_i^2)\cdot w_i^2+\delta^2$

So, in the case of a linear forecast and known weights , we can either include or exclude terms. It's logical to include terms $w_i\cdot f_i$ with those factors where the noise variance is smaller than the variance of the least noisy factor . However, apart from the options of "including" or "excluding", there's also the option of including with a different, smaller weight in magnitude. Additionally, the forecasting model doesn't necessarily have to be linear. The correct solution to the problem appears more intricate; in reality, we can always extract some benefit from a factor if it holds new information, even if it's highly noisy.

Let's consider having two unbiased forecasts and with errors:

$\; mse_0 = D(target - predict_0) = \sigma_0^2,\\ mse_1=D(target - predict_1) = \sigma_1^2.$

Then, if they were completely independent, a new, more accurate forecast could be constructed from them as:

$predict_c = {m_0 \cdot predict_0 + m_1 \cdot predict_1 \over m_0 + m_1},\\ m_0 = 1/\sigma_0^2,\; m_1 = 1/\sigma_1^2.$

The error of this forecast would be:

$\sigma_c^2 = {1 \over 1/\sigma_0^2 + 1/\sigma_1^2}$

That is, $m_c = 1/\sigma_c^2 = m_0 + m_1.$

Why this holds true for independent forecasts is suggested for self-exploration. This scenario resembles, for instance, two independent groups of researchers providing their estimations of the Higgs boson's mass with uncertainties, and the need arises to combine them.

In our case, the estimations are dependent, and in the errors:

$target - predict_0 = -w_1\cdot g_1 + \nu_1, \\ target - predict_1= - w_1\cdot \zeta_i + \nu_1$

There's a common part $\nu_1$ - the common irreducible error for these two forecasts. When combining, we essentially combine only two independent parts $-w_1\cdot g_1$ and $-w_1 \cdot \zeta_1$ , yielding the result:

$predict_c= F_0 + {m_0\cdot 0 + m_1\cdot (w_1 \cdot f_i) \over m_0 + m_1}=\\=F_0 + {1\over m_0/m_1+1}\cdot w_1\cdot f_1$

Where

$m_0 = 1/w_1^2,\; m_1= 1/(w_1^2\cdot z_1^2).$

Thus:

$predict_c = F_0 + {1 \over z_1^2+1}\cdot w_1\cdot f_1$

And the error of such a forecast will be:

$\sigma_c^2 = w_1^2 {z_1^2\over z_1^2 + 1} + \delta_1^2$

This is less than the errors $\sigma_0^2=w_1^2 + \delta_1^2$ and $\sigma_1^2=w_1\cdot z_1^2 + \delta_1^2$ of both forecasts, and

The final formula for the best linear forecast looks like this:

$predict = \sum_{i=1}^m {1\over z_i^2 + 1} \cdot w_i \cdot f_i$

And the error of this forecast is:

$D(target - predict) = \sigma^2=\sum_{i=1}^m {z_i^2\over z_i^2+1} \cdot w_i^2+\delta^2$

So, with known weights, all factors are useful. But when weights are unknown and the training pool is not sufficiently large, some factors need to be discarded.

Weights can be estimated by the formula:

$w'_i= \mathrm{avg}(target \cdot f_i)/\mathrm{avg}(f_i^2)$

Let's see what this expression equals in the limit when the training log is large, and the average can be replaced with the mathematical expectation. If all factors are initially normalized so that their mean is zero:

$M(target \cdot f_i) =\\= M((\ldots + w_i\cdot g_i)\cdot (g_i + \zeta_i)) =\\= M(w_i\cdot g_i^2) = w_i$

And the mean square of the factor is:

$M((g_i + \zeta_i)^2) = M(g_i^2 + \zeta_i^2) = 1 + z_i^2$

Thus, the expression $w'_i = \mathrm{avg}(target \cdot f_i)/\mathrm{avg}(f_i^2)$ in the limit equals , precisely what needs to be substituted into the formula. The value will be calculated with an error, deviating from - due to the finiteness of the training pool (the normalization won't be perfect, and the sample averages will differ from the true mathematical expectations). Let an estimate of the mean square of the relative error be given:

$\epsilon_i=\left( { w'_i \over w_i / (1+z_i^2)}-1\right),\;\; d^2_i=M(\epsilon_i^2).$

If we don't include the term $w'_i\cdot f_i$ in the forecast, the additional term to the error square (from losing the true term $w_i\cdot g_i$ ) equals If instead of $w_i\cdot g_i$ , we include $w'_i\cdot f_i$ , the additional term to the error square equals:

$M((w'_i\cdot f_i - w_i\cdot g_i)^2) =\\=M\left(\left({w_i \over 1+z_i^2}\cdot (1 + \epsilon_i)\cdot(g_i + \zeta_i) - w_i\cdot g_i\right)^2\right) = \\ = w_i^2\cdot M\left(\left(\left({1 + \epsilon_i\over 1+z_i^2} - 1\right)\cdot g_i + \left({1 + \epsilon_i\over 1+z_i^2}\right)\cdot \zeta_i \right)^2 \right)$

Here we:

pulled out
divided the expression in brackets into two parts, which are independent random variables with a mean of 0.

If this expression is greater than it's better to discard the factor. The final expression simplifies to:

$w_i^2 \cdot\left({1 + d_i^2 \over (1 + z_i^2)^2} - {2 \over 1 + z_i^2}+1 + {1+d_i^2 \over (1+z_i^2)^2} z_i^2 \right) = \\ = w_i^2 \cdot\left({d_i^2 + z_i^2 \over 1 + z_i^2} \right)$

Therefore, if the relative error of the estimate is greater than 1, the factor is better off discarded. The error of can be estimated, for instance, by the bootstrap method.

From this answer, we can derive the following intuitive idea - if during gradient descent (regular or stochastic) at the last iterations, a weight in the model changes its sign, it's better to set it to 0.

Quadratic Loss Function and Mutual Information

Usually, the prediction task is formulated as minimizing the error:

ML-task №3.1: Based on the given training pool, train a model $predict=\mathcal{P}(f_1, \ldots)$ that minimizes the average error. The quality of the prediction will be measured by the average error on the hidden test pool.

But it's possible to try formulating the prediction task as a maximization of MI.

ML-task №3.2: Based on the given training pool, train a model $\mathcal{P}(f_1, \ldots)$ such that

the value predict has the maximum possible mutual information with
i.e. $\mathrm{MI}(predict, target)\to \mathrm{max}$ ;
is an unbiased forecast of , meaning the expectation of the discrepancy $\xi = predict - target$ equals 0 under the condition for any .

This is a brief but not entirely correct formulation, requiring some clarifications. Specifically, the following points need clarification:

In what sense can the pair be interpreted as a pair of dependent random variables?
The requirement of unbiasedness seems unattainable if the dataset on which we train and test is finite and fixed.

These points can be resolved straightforwardly. During testing, we sample an example from a potentially infinite pool and get a pair of random variables And unbiasedness should be understood in the way it's commonly done in mathematical statistics in regression problems - unbiasedness on average over all possible training and test pools, not on specific pool data.

More details

The deterministic function $\mathcal{P}(f_1, \ldots, f_k)$ is interpreted as a random variable as follows: we sample a row from the test pool, extract a set of factors $(f_1, \ldots, f_k)$ , and the . Then we substitute these factors into the function and get the value and a pair of dependent random variables .

The requirement of unbiasedness should be understood as an average unbiasedness when considering the training and test pools as random variables. That means a specific finite training pool will certainly yield a model with a biased forecast - the average value of the difference will not be zero on average for a random example from a potentially infinite test pool. However, one can consider the difference , where the average is taken over all possible models that could be obtained by training on hypothetical training pools and testing on hypothetical test pools. Another way to justify unbiasedness is by requiring it in the limit, as the size of the training pool tends to infinity. These interpretations of unbiasedness give a chance for the existence of a solution to ML-task №3.2.2. However, to be honest, neither engineers nor ML theorists pay much attention to the bias issue, as is commonly done in methods of mathematical statistics. ML practitioners acknowledge this and openly prefer to test and evaluate their methods on artificial or real problems using error metrics, without analyzing their bias.

But I needed the requirement of unbiasedness to reformulate the prediction task in terms of maximizing MI.

So, we'll allow ourselves to perceive the test pool as a source of random examples and use the terminology of probability theory.

Definition 3.2: A loss function equal to the expected value of the squared error $M_{\xi^2}$ will be referred to as– ошибкой or squared error or MSE (Mean Squared Error). And a loss function $M_{|\xi|^p}$ will be referred to as – ошибкой.

Statement 3.1: Suppose your model in the ML-task №3.2.2 or ML-task №3.2.1 has the discrepancy $\xi = predict - target$ possessing two properties:

It is a normal variable with a zero mean (meaning the forecast is unbiased) for any fixed value of .
It has a variance that is independent of .

Then the ML-task №3.1 and ML-task №3.2 problems are equivalent for Loss = MSE, meaning the "maximize MI" task provides the same solution as the "minimize MSE-error" task.

Of course, these properties described in the statement are rarely encountered in practice, but nonetheless, this fact is interesting.

First, these properties are attainable when the vector of factors and the $(f_1, f_2, \ldots, f_n, target)$ constitutes a measurement of a multivariate normal variable. This occurs specifically when the is a linear combination of several independent Gaussian variables, some of which are known and provided as factors. In this case, seeking the forecast as a linear combination of these given factors is natural.

In this case,

$\mathrm{MI}(target, predict) = \log({\sigma_t^2 / \sigma_e^2})$ ,

where $\sigma_e^2$ is the average value of the squared forecast error, that is $M_{\xi^2} = M_{{(target - predict)}^2}$ , and $\sigma_t^2$ is the variance of the (see task 2.8 about the mutual information of two dependent normal variables). Clearly, in this scenario, maximizing $\mathrm{MI}$ is equivalent to minimizing $M_{\xi^2}=\sigma_e^2$ .

It should be understood that while a pure, unbiased Gaussian for the error $\xi$ that does not depend on is not encountered in practice, the distribution of the given a fixed often resembles a Gaussian "bell curve" centered at . The statement about equivalence is almost true in such cases. Specifically, the task of maximizing MI is equivalent to the task of minimizing the error in an -like metric, where the averaging is weighted and somehow dependent on .

To be precise, if the bell curve of the $\rho_\xi$ distribution is unimodal, symmetric, and with a quadratic peak, then an equivalent task regarding the maximization of MI can be formulated. We'll discuss this below.

For now, let's attempt to prove the statement about the equivalence of the "maximize MI" and "minimize L2" tasks for the case described in Statement 3.1.

Let's introduce the abbreviations: t = target, p = predict.

The proof is based on simply expressing the value of $\mathrm{MI}$ in the following form:

$\mathrm{MI}(p, t) = H(t) - \int H(t | p = x) \rho_{p}(x) dx$

The value is independent of the forecast and is $C + 0.5\cdot \log(D(t)).$ The value is $C + 0.5\cdot \log(D(t|p=x)),$ whererepresents the variance of the predicted quantity given a particular prediction. According to the second condition of the statement, it is constant. In the case of an unbiased forecast, this is $M_{\xi^2}$ (i.e., precisely the squared error) given

The expression $\int \ldots \rho_{p}(x) dx$ essentially represents averaging over the pool.

If $M_{\xi^2}$ is independent of then we get the required statement. Indeed,

$\mathrm{MI}(p, t) = С + 0.5\cdot \log(D(t)) - \int (C + 0.5 \log(\mathrm{mse})) \rho_{p}(x) dx = \\ = 0.5 \cdot \log(D(t) / \mathrm{mse})$

Maximizing this expression is equivalent to minimizing the MSE. End of proof.

For a better understanding, let's elaborate further on the expression:

$\mathrm{MI}(p, t) =\\= H(t) - \int H(t | p = x) \rho_{p}(x) dx =\\= H(t) - \int \rho_{t}(y | p = x) \log(1/\rho_{t}(y | p = x)) \rho_{p}(x) dx dy =\\ = H(t) - \int \log(1/\rho_{t}(y | p = x)) \cdot \rho_{t,p}(x, y) dx dy$

The integration

$\int \ldots (\rho_{t,p}(x, y) dx dy$

again corresponds to simply averaging over the pool, and the expression $\log(1/\rho_{t}(y | p = x))$ is what should be interpreted as the error value. If we transition to the discretized case and recall Huffman encoding, $\log(1/P(t= y | p = x))$ is the number of bits required to write the code for the value (with some precision $\varepsilon$ ) given the value . If the forecast is unbiased and it is given to us, to encode with a certain precision, it is simpler to write the code for the discrepancy $\xi=t- p$ , which is a random variable with a zero mean and a smaller variance than the variance of . These considerations lead to another formulation of the forecasting problem as a maximization of MI:

ML-task №3.3: Train a model $predict(f_1, \ldots, f_k)$ based on the given training pool, such that encoding the discrepancy within an accuracy of $\varepsilon$ requires the minimum number of bits.

In this task, the implication is the naive encoding of numbers, where all significant digits are recorded. For instance, assuming a fixed precision of $\varepsilon = 0.000001$ , a number like $-0.000123456789\pm 0.000001$ is logically encoded as "-123". Here, one bit is spent on the sign (+ or - at the beginning), and we disregard all digits starting from the seventh place after the decimal point. We only record the significant figures without listing leading zeros. The last digit in the code is understood to be at the sixth place after the decimal point. In this encoding, the smaller the average error, the fewer bits are needed to encode all errors in the test pool. The value of $\varepsilon$ must be sufficiently small. Beyond this naive encoding, it's crucial to apply Huffman encoding to further compress the data based on differences in the probabilities of various errors.

In this formulation, we are, in a sense, forced to define our own Loss function. Some tend to view this as a criterion for choosing the right Loss function: if you minimize mse, it's good when $\log(1/P(t= y | p = x))$ tends towards $A \cdot (y - x)^2 + B$ as the training and test pools grow, meaning the discrepancy distribution approximates normality. When minimizing L1-error, it's favorable if $\log(1/P(t= y | p = x))$ tends towards $A\cdot |y - x| + B$ , indicating the discrepancy distribution approximates the Laplace distribution. In general, approximate equality $P(t = y| p=x) \approx e^{-A \cdot Loss(y,x) + B}$ is expected. If not, either you haven't completed the ML task, or your problem doesn't fall into the category of good problems.

Apparently, under certain conditions, these arguments hold in the other direction as well. If you have an ideal solution to ML-task №3.3, studying the discrepancy distribution for its solution reveals the Loss function that should be used to extract the maximum information from the signal.

Log-Likelihood and Mutual Information

An example from real life: Implement a deterministic function $\mathcal{P}(пол, возраст, последние\ 10\ поисковых\ запросов, \ldots)$ predicting the probability, p , that a user will click on a given advertisement.

Tasks of this type, where you need to forecast a Boolean variable (a variable that takes "Yes" or "No" values), are referred to as binary classification problems.
To solve them, the maximum likelihood method is typically used. Specifically, it is assumed that the prediction, , should return a real number from 0 to 1, corresponding to the probability that the (user clicks on the ad). When training the predictor on the training set, internal model parameters (also known as weights) can be adjusted to maximize the probability of observing what is in the training set.

Usually, it's not just the probability that's maximized but a combination of this probability and a regularization component. There are no restrictions on how developers design this regularization component. Moreover, the training algorithm can be anything; what matters are just two things:

During training, the algorithm doesn't "see" data from the test pool.
Predictors are compared based on the probability estimates of events in the test pool.

The probability of observing what we see in the pool, when applied to the model, is referred to as the model likelihood. In other words, we talk about the 'probability of an event' and 'model likelihood,' but we don't talk about the 'probability of a model' or 'event likelihood.'

Here's an example test pool consisting of three rows:

i	f₁	f₁	f₁	target	predict= P(target=1)	P(target=0)
1	...	...	...	0
2	...	...	...	1
3	...	...	...	0
			$\mathrm{Likelihood}=(1-p_1)\cdot p_2\cdot(1-p_3)$

It's more convenient to work with the LogLikelihood value:

$\mathrm{LogLikelihood} = \log((1 - p_1)\cdot p_2\cdot (1 - p_3)) = \log(1 - p_1) + \log (p_2) + \log(1 - p_3)$

Rows with contribute to the total Log-Likelihood as $\log(predict)$ , and rows with contribute as $\log(1 - predict)$ .

In a simplified form, the binary classification problem looks like this:

ML-task №3.4: Given a training log. Find a deterministic function $predict(f_1,f_2,\ldots),$ so that the value of $\mathrm{LogLikelihood}(predict, target)$ on the test pool is maximized.

Let's formulate a similar task in terms of maximizing MI.

ML-task №3.5: Find a deterministic function $p=predict(f_1,f_2,\ldots),$ such that a random discrete variable $\xi$ taking values 0 and 1 with probabilities $\{p,\; 1 - p\},$ has the maximum possible value of mutual information $\mathrm{MI}(\xi, target)$ with the variable.

Statement 3.2: If your model is such that $\xi = predict - target$ is a random variable with a zero mean (in other words, the prediction is unbiased), then ML-task №3.2.2 and ML-task №3.2.1 are equivalent. That is, the task "maximize MI(target, predict)" gives the same answer as the task "maximize LogLikelihood."

The requirement that the prediction is unbiased, or in other words, doesn't require calibration, isn't a complex demand. In classification tasks, if you're using Gradient Boosted Trees or neural networks with appropriate hyperparameters (learning rate, number of iterations), the prediction becomes unbiased. Specifically, if you take events with $predict \in [x - \varepsilon, x + \varepsilon],$ you get a set of events where:

$p_{fact} = { \mathrm{number\_of\_lines\_with\_target\_1} \over \mathrm{number\_of\_lines}} = {\mathrm{clicks} \over \mathrm{impressions}}\approx x$

In classification tasks, I'm accustomed to calling rows where the target = 1 as clicks and rows with target = 0 as non-clicks. Clicks plus non-clicks constitute the set of all events, termed impressions. The actual ratio of clicks to impressions is called CTR — Click Through Rate.

To prove Statement 3.2, let's utilize the solution to the problem.

Task 3.10. How can the value of $\mathrm{MI}(\xi,\; \mu)$ be estimated based on N measurements of two random variables - a discrete variable $\xi$ taking values from 1 to M, and a boolean random variable $\mu$ ?

One way to think about this task: $\xi$ is a categorical variable related to an advertising announcement; its values can be interpreted as class identifiers, while $\mu = \mathrm{IsClick}$ indicates whether a click occurred. The data regarding the measurements of pairs $(\xi, \mu)$ represents a log of clicks and non-clicks.

To solve this problem, it's convenient to use the formula:

$\mathrm{MI}(\xi,\mu) = H(\mu) - H(\mu | \xi)=H(\mu)-{\sum}_i P(\xi=i)\cdot H(\mu|\xi=i)$

Value $H(\mu)=H(\mathrm{ctr}_{0})$ , where $\mathrm{ctr}_{0} = \mathrm{ctr}_{total} = \mathrm{clicks}_{total} / \mathrm{impressions}_{total}$ - the average CTR over the entire log.

And $H(\mu | \xi = i) = H(\mathrm{ctr}_i)$ , where $\mathrm{ctr}_{i} = \mathrm{clicks}_{i} / \mathrm{impressions}_{i}$ - CTR for events where $\xi = i$ , naturally called CTR in class i. Substituting these into the formula and we get:

$\mathrm{MI}(\mu, \xi) = H(\mu) - H(\mu | \xi) = \\ = H(\mathrm{ctr}_{0}) - \displaystyle\sum_{i\in classes} { \mathrm{impressions}_i \over \mathrm{impressions}_{total} } \cdot H(\mathrm{ctr}_i) = \\ = - (\mathrm{ctr}_{0}\cdot \log(\mathrm{ctr}_{0}) + (1 - \mathrm{ctr}_{0})\cdot \log(1 - \mathrm{ctr}_{0})) +\\ + \displaystyle\sum_{i\in classes} {\mathrm{impressions}_i \over \mathrm{impressions}_{total}} \cdot ( \mathrm{ctr}_{i}\cdot \log(\mathrm{ctr}_{i}) + (1 - \mathrm{ctr}_{i})\cdot \log(1 - \mathrm{ctr}_{i}))$

Let's focus on the first term and express it as a sum over classes:

$H(\mu) = - \left(\displaystyle{\mathrm{clicks}_{total} \over \mathrm{impressions}_{total}} \log(\mathrm{ctr}_{0}) + \displaystyle{\mathrm{notclicks}_{total} \over \mathrm{impressions}_{total}}\cdot \log(1 - \mathrm{ctr}_{0})\right) = \\$ $= - \displaystyle\sum_{i \in classes}\left({\mathrm{clicks}_i \over \mathrm{impressions}_{total}} \log(\mathrm{ctr}_{0}) + {\mathrm{notclicks}_i \over \mathrm{impressions}_{total}}\cdot \log(1 - \mathrm{ctr}_{0})\right) =$ $- \displaystyle\sum_{i \in classes}\left({\mathrm{ctr}_i \cdot \mathrm{impressions}_i \over \mathrm{impressions}_{total}} \log(\mathrm{ctr}_{0}) + {(1 - \mathrm{ctr}_i)\cdot \mathrm{impressions}_i \over \mathrm{impressions}_{total}} \log(1 - \mathrm{ctr}_{0})\right).$

Substituting this into the expression for MI, and combining both parts into one sum over classes, we get the final expression for MI:

$\displaystyle\sum_{i \in classes} { \mathrm{impressions}_i \over \mathrm{impressions}_{total}} \cdot \left(\mathrm{ctr}_{i}\cdot \log\left({\mathrm{ctr}_{i} \over \mathrm{ctr}_{0}}\right) + (1 - \mathrm{ctr}_{i})\cdot \log\left({1 - \mathrm{ctr}_{i} \over 1 - \mathrm{ctr}_{0}}\right)\right) = \\ = \displaystyle{1 \over \mathrm{impressions}_{total}} \displaystyle\sum_{e \in \mathrm{impressions}} \mathrm{ctr}_{i(e)}\cdot \log{\left({\mathrm{ctr}_{i(e)} \over \mathrm{ctr}_{0}}\right)} + (1 - \mathrm{ctr}_{i(e)})\cdot \log{\left({1 - \mathrm{ctr}_{i(e)} \over 1 - \mathrm{ctr}_{0}}\right)}$

In the last equality, we replaced summation over classes with summation over log entries to show the similarity of the formula to the LogLikelihood formula.

When the classes are merely prediction bins and the prediction is unbiased (meaning the average prediction in a bin matches the real $\mathrm{ctr}$ in that bin), we have:

$\mathrm{LogLikelihood(predict)}=\\ = \sum_{e\in \mathrm{impressions}}\mathrm{ctr}_{i(e)}\cdot \log(\mathrm{ctr}_{i(e)}) + (1-\mathrm{ctr}_{i(e)})\cdot\log(1-\mathrm{ctr}_{i(e)})$

And if the prediction equals a constant $\mathrm{ctr}_0$ , the likelihood expression becomes:

$\mathrm{LogLikelihood}(\mathrm{predict}=\mathrm{ctr}_0)=\\ = \sum_{e\in \mathrm{impressions}}\mathrm{ctr}_{0}\cdot \log(\mathrm{ctr}_{0}) + (1-\mathrm{ctr}_{0})\cdot\log(1-\mathrm{ctr}_{0})=\\= \sum_{e\in \mathrm{impressions}}\mathrm{ctr}_{i(e)}\cdot \log(\mathrm{ctr}_{0}) + (1-\mathrm{ctr}_{i(0)})\cdot\log(1-\mathrm{ctr}_{0})$

Replacing $\mathrm{ctr}_0$ with $\mathrm{ctr}_{i(e)}$ is valid since the expressions with logarithms are constant, and the average value of $\mathrm{ctr}_{i(e)}$ over all impressions equals $\mathrm{ctr}_0$ .

Here, we see that the final expression for MI is simply the normalized difference between two expressions for LogLikelihood:

$\mathrm{MI}(\xi, \mu) = \ \mathrm{MI}(predict, \mu) =\\ \ {1 \over \mathrm{impressions}_{total}}\cdot (\mathrm{LogLikelihood}(predict) - \mathrm{LogLikelihood}(predict = \mathrm{ctr}_{0})$

Therefore, in the case of an unbiased prediction, the $\mathrm{MI}(predict, target)$ is a linear function of the LogLikelihood.

By the way, the quantity $\mathrm{LogLikelihood}(predict_1) - \mathrm{LogLikelihood}(predict_2)$ is called the Log Likelihood Ratio of two predictors, and it's naturally normalized by the number of events (impressions). often represents a basic prediction, in our case, a constant prediction. It's often worthwhile to monitor the graph of LogLikelihoodRatio / impressions, rather than LogLikelihood / impressions, using a robust (simple, reliable, not easily broken) prediction based on a few factors as the baseline . Sometimes, using $\mathrm{LogLikelihoodRatio} / \mathrm{impressions} \cdot \mathrm{ctr}_0^{\gamma}$ for some $\gamma$ can eliminate correlation or anti-correlation with $\mathrm{ctr}_0$ and better visualize prediction break points.

Thus, for an unbiased prediction, the MI between the prediction and the signal equals the normalized Log Likelihood Ratio of your prediction and the best constant prediction.

Evaluation of Mutual Information = Machine Learning

Two statements — 3.1 and 3.2 — assert that Mutual Information is a quality metric that, under certain assumptions, corresponds to two metrics in prediction tasks — the mean squared error in predicting a real value with a normal distribution and LogLikelihood in binary classification tasks.

The Mutual Information (MI) itself cannot be used as a loss function because it's not a metric on data, i.e., it doesn't represent the sum of loss function values across elements in a pool. The notion of "correspondence" can be clarified as follows: practically, almost all loss functions ultimately aim to maximize the Mutual Information between the predict and target, albeit with different additional terms.

Perhaps the following two statements (again, without proof) shed light on this:

Statement 3.3: If you have a prediction based on factors $f_1,\ldots,f_k$ , and there's a new factor $f_{k+1},$ such that $\mathrm{MI}(\{f_{k+1}, predict\}, target) > \mathrm{MI}(predict, target),$ then with a sufficiently large training pool, this factor will reduce your loss function if it's normal. A Loss-function is considered normal if it decreases when, in any element of the pool, the predict value approaches the target. Mean squared error (MSE), - error, LogLikelihood — they all represent normal Loss-functions. Going forward, let's assume the loss function is normal.

Any monotonic transformation of the prediction will be referred to as the calibration of the prediction.

Statement 3.4 (requires specification of conditions): If you find a change in weights (or internal parameters) of your model that increases $\mathrm{MI}(predict, target),$ then after proper calibration of the prediction, your Loss-function will increase.

In these statements, MI cannot be replaced with any loss function. For instance, if you make weight changes in your model that decrease the - error, it doesn't imply that the - error will decrease even after proper calibration of the prediction to fit . The distinctness of MI is associated with the fact that, as mentioned earlier, it's not exactly a loss function and inherently allows any calibration (meaning it doesn't change under arbitrary strictly monotonic calibration of the prediction).

Task 3.11: Prove that in the case where the $target=\mathcal{P}(f_1,f_2,\ldots,w_1,w_2,\ldots) + \nu$ , where $\nu$ is random noise, and the model matches reality, as the training pool size increases, the weights tend toward the correct values for both and Loss-functions. Additionally, if the noise has a symmetric distribution, both Loss-functions provide an unbiased prediction.

Task 3.12: Provide an example of a model and a real target where the and loss functions yield different predictions even on a very large training pool, such that one cannot be transformed into the other by any monotonic transformation (i.e., the calibration of one prediction cannot be achieved from the other).

Statement 3.5: The task of estimating $mi = \mathrm{MI}(\{f_1,\ldots, f_k\}, target)$ is equivalent to the task of constructing a prediction $predict=\mathcal{P}(f_1,\ldots, f_k)$ in some Loss-function.

This statement suggests that the true value of mi is approximately equal to the supremum of $\mathrm{MI}(predict, target)$ for all pairs (ML method, Loss-function), where ML method ::= ("model structure", "method of getting model weights"), "method of getting model weights" ::= ("algorithm", "algorithm hyperparameters"), and the equality is more accurate the larger the training pool.

Essentially, the pair (ML method, loss function) that yields the highest value of $\mathrm{MI}(predict, target)$ close to mi is the model closest to reality, that is, how $f_1,\ldots,f_k$ and target are actually related.

In summary: we've formulated two profound connections between prediction tasks and MI:

Firstly, maximizing MI somewhat corresponds to minimizing a certain loss function.
Secondly, "MI estimation" = "ML", namely, estimating $\mathrm{MI}(\{f_1,\ldots, f_k\}, target)$ is equivalent to constructing a prediction $\mathcal{P}(f_1,\ldots, f_k)$ for some Loss-function. The ML method and Loss-function that yield the maximum $\mathrm{MI}(predict, target)$ represent the most plausible model.

Tags:

Hubs: