
Когда я изучал обработку аудиосигналов, мой мозг начал проводить аналогии с процедурным генерированием карт. В статье излагаются принципы, связывающие обработку сигналов с генерированием карт. Не думаю, что открыл что-то новое, но некоторые выводы были для меня в новинку, поэтому я решил записать их и поделиться с читателями. Я рассматриваю только простые темы (частоту, амплитуду, цвета шума, использование шума) и не затрагиваю другие темы (дискретные и непрерывные функции, фильтры FIR/IIR, быстрое преобразование Фурье, комплексные числа). Математика статьи в основном связана с синусоидами.
Эта статья посвящена концепциям, начиная с самых простейших и заканчивая более сложными. Если вы хотите перейти сразу к генерированию рельефа с помощью функций шума, то изучите другую мою статью.
Я начну с основ использования случайных чисел, а потом перейду к объяснению работы одномерных ландшафтов. Те же концепции работают для 2D (см. демо) и 3D. Попробуйте перемещать ползунок [в оригинале статьи], чтобы посмотреть, как единственный параметр может описывать различные типы шума:
GIF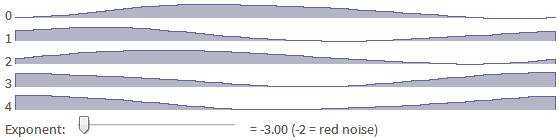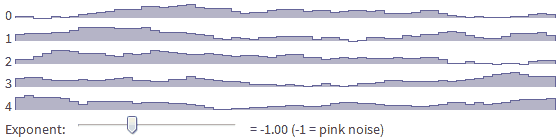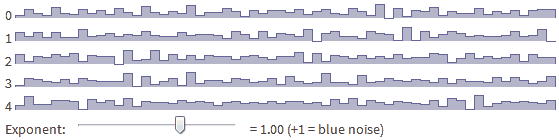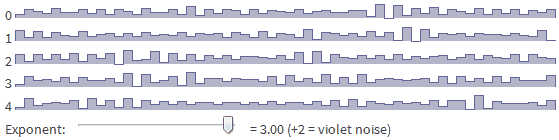

Из этой статьи вы узнаете:
- как генерировать похожие ландшафты всего в 15 строках кода
- что такое красный, розовый, белый, синий и фиолетовый шум
- как можно использовать функции шума для процедурного генерирования карт
- как применяются смещение средней точки, шум Перлина и фрактальное броуновское движение
Кроме того, я проведу эксперименты с 2D-шумом, в том числе создам 3D-визуализацию двухмерной карты высот.
1. Почему полезна случайность?
Процедурное генерирование карт нужно нам для получения наборов выходных данных, имеющих что-то общее, и что-то отличающееся. Например, в всех картах Minecraft есть много общего: области биомов, размер сетки, средние размеры биомов, высоты, средние размеры пещер, процентное соотношение каждого типа камней, и т.д. Но у них есть и различия: расположение биомов, места и формы пещер, размещение золота и прочее. Как дизайнеру вам нужно решить, какие аспекты должны остаться одинаковыми, а какие должны отличаться, и брать степень этого различия.
Для отличающихся аспектов мы обычно используем генератор случайных чисел. Давайте создадим сверхпростой генератор карт: он будет генерировать линии по 20 блоков, и один из блоков будет содержать сундук с золотом. Давайте опишем несколько карт, которые нам нужны (значком «x» отмечено сокровище):
карта 1 ........x...........
карта 2 ...............x....
карта 3 .x..................
карта 4 ......x.............
карта 5 ..............x.....Заметьте, как много общего в этих картах: они все состоят из блоков, блоки находятся на одной линии, линия имеет длину 20 блоков, есть два типа блоков и ровно один сундук с сокровищем.
Но есть один отличающийся аспект — местонахождение блока. Он может находиться в любой позиции, от 0 (слева) до 19 (справа).
Мы можем использовать случайное число для выбора позиции этого блока. Проще всего будет использовать однородный выбор случайного числа из диапазона от 0 до 19. Это значит, что вероятность выбора любой позиции от 0 до 19 одинакова. В большинстве языков программирования есть функции для однородного генерирования случайных чисел. В Python это функция
random.randint(0,19), но в статье мы будем использовать запись random(0,19). Вот пример кода на Python:def gen():
map = [0] * 20 # создаём пустую карту
pos = random.randint(0, 19) # выбираем точку
map[pos] = 1 # помещаем туда сокровище
return map
for i in range(5): # создаём 5 разных карт
print_chart(i, gen())Но предположим, что нам нужно, чтобы на картах сундук с большей вероятностью находился слева. Для этого нам нужно неоднородный выбор случайных чисел. Существует много способов реализовать его. Один из них — выбрать случайное число однородным способом, а затем сместить его влево. Например, можно попробовать
random(0,19)/2. Вот код Python для этого:def gen():
map = [0] * 20
pos = random.randint(0, 19) // 2
map[pos] = 1
return map
for i in range(5):
print_chart(i, gen())Но на самом деле я хотел не совсем этого. Я хотел, чтобы сокровища иногда были справа, но более часто слева. Ещё один способ переместить сокровища влево — возвести число в квадрат, сделав что-то вроде
sqr(random(0,19))/19. Если оно равно нулю, то 0 в квадрате, поделённый на 20, равен 0. Если оно равно 19, то 19 в квадрате, поделённое на 19, будет равно 19. Но в промежутке, если число равно 10, то 10 в квадрате, поделённое на 19, равно 5. Мы сохранили диапазон от 0 до 19, но переместили промежуточные числа влево. Такое перераспределение само по себе является очень полезной техникой, в предыдущих проектах я использовал квадраты, квадратные корни и другие функции. (На этом сайте есть стандартные функции изменения формы, применяемые в анимациях. Наведите курсор на функцию, чтобы посмотреть демо.) Вот код Python использования возведения в квадрат:def gen():
map = [0] * 20
pos = random.randint(0, 19)
pos = int(pos * pos / 19)
map[pos] = 1
return map
for i in range(1, 6):
print_chart(i, gen())Ещё один способ перемещения объектов влево — сначала случайным образом выбрать предел диапазона случайных чисел, затем случайно выбрать число от 0 до предела диапазона. Если предел диапазона равен 19, то мы можем поместить число куда угодно. Если предел диапазона равен 10, то числа можно разместить только в левой части. Вот код Python:
def gen():
map = [0] * 20
limit = random.randint(0, 19)
pos = random.randint(0, limit)
map[pos] = 1
return map
for i in range(5):
print_chart(i, gen())Существует много способов получения однородных случайных чисел и превращения их в неоднородные, имеющие нужные свойства. Как гейм-дизайнер, вы можете выбирать любое распределение случайных чисел. Я написал статью о том, как использовать случайные числа для определения урона в ролевых играх. Там есть разные примеры хитростей.
Подведём итог:
- Для процедурного генерирования нам нужно решить, что останется одинаковым, а что будет меняться.
- Случайные числа полезны для заполнения изменяющихся частей.
- Однородно выбираемые случайные числа можно получить в большинстве языков программирования, но часто нам требуются неоднородно выбираемые случайные числа. Для их получения существуют разные способы.
2. Что такое шум?
Шум — это серия случайных чисел, обычно расположенных на линии или в сетке.
При переключении на канал без сигнала на старых телевизорах мы видели на экране случайные чёрные и белые точки. Это шум (их открытого космоса!). При настройке на радиоканал без станции мы тоже слышим шум (не уверен, появляется ли он из космоса, или откуда-то ещё).
При обработке сигналов шум обычно является нежелательным аспектом. В шумной комнате сложнее услышать собеседника, чем в тихой. Аудиошум — это случайные числа, выстроенные в линию (1D). На зашумлённом изображении сложнее увидеть рисунок, чем на чётком. Графический шум — это случайные числа, расположенные в сетке (2D). Можно создавать шум в 3D, 4D, и так далее.
Хотя в большинстве случаев мы пытаемся избавиться от шума, многие естественные системы выглядят шумными, поэтому для генерирования чего-то, похожего на естественное, нам нужно добавить шум. Хотя реальные системы и выглядят шумными, но в их основе обычно заложена структура. Добавляемый нами шум не будет иметь той же структуры, но он гораздо проще, чем программирование симуляции, поэтому мы используем шум, и надеемся, что конечный пользователь этого не заметит. Об этом компромиссе я расскажу позже.
Давайте рассмотрим простой пример полезности шума. Допустим, у нас есть одномерная карта, которую мы сделали выше, но вместо одного сундука с сокровищем нам нужно создать ландшафт с долинами, холмами и горами. Давайте начнём с использования однородного выбора случайных чисел в каждой точке. Если
random(1,3) равно 1, мы будем считать это долиной, если 2 — холмами, если 3 — горами. Я использовал случайные числа для создания карты высот: для каждой точки массива я сохранил высоту ландшафта. Вот код Python для создания ландшафта:for i in range(5):
random.seed(i) # даёт каждый раз одинаковые результаты
print_chart(i, [random.randint(1, 3)
for i in range(mapsize)])
# примечание: я использую синтаксис генератора списков Python:
# output = [abc for x in def]
# это упрощённая запись такого кода:
# output = []
# for x in def:
# output.append(abc)Хм, эти карты выглядят «слишком случайными» для наших целей. Возможно, нам нужны более обширные области долин или холмов, а горы не должны быть такими же частыми, как долины. Ранее мы видели, что однородный выбор случайных чисел нам может не совсем подойти, иногда нам требуется неоднородный выбор. Как решить эту проблему? Можно использовать какой-нибудь случайный выбор, в котором долин появляются чаще, чем горы:
for i in range(5):
random.seed(i)
print_chart(i, [random.randint(1, random.randint(1, 3))
for i in range(mapsize)])Это уменьшает количество гор, но не создаёт никаких интересных рисунков. Проблема такого неоднородного случайного выбора в том, что изменения происходят в каждой точке по отдельности, а нам нужно, чтобы случайный выбор в одной точке как-то был связан со случайными выбора в соседних точках. Это называется когерентностью.
И тут нам пригодятся функции шума. Они дают нам набор случайных чисел вместо одного числа за раз. Здесь нам нужна функция 1D-шума для создания последовательности. Давайте попробуем использовать функцию шума, изменяющую последовательность однородных случайных чисел. Есть разные способы сделать это, но мы используем минимум двух соседних чисел. Если исходный шум равен 1, 5, 2, то минимум (1, 5) равен 1, а минимум (5, 2) равен 2. Поэтому конечный шум будет равен 1, 2. Заметьте, что мы устранили высокую точку (5). Также заметьте, что в получившемся шуме на одно значение меньше по сравнению с исходным. Это значит, что при генерировании 60 случайных чисел на выходе будет только 59. Давайте применим эту функцию к первому набору карт:
def adjacent_min(noise):
output = []
for i in range(len(noise) - 1):
output.append(min(noise[i], noise[i+1]))
return output
for i in range(5):
random.seed(i)
noise = [random.randint(1, 3) for i in range(mapsize)]
print_chart(i, adjacent_min(noise))По сравнению с предыдущими картами здесь получились области долин, холмов или гор. Горы чаще появляются рядом с холмами. И благодаря способу изменения шума (выбор минимума), долины чаще встречаются, чем горы. Если бы мы взяли максимум, то картина была бы противоположной. Если бы мы хотели, чтобы частыми не были ни долины, ни горы, мы выбрали бы вместо минимума или максимума среднее.
Теперь у нас есть процедура модификации шума, на входе получающая шум, и создающая новый, более сглаженный шум.
А давайте попробуем запустить её снова!
def adjacent_min(noise): # так же как раньше
output = []
for i in range(len(noise) - 1):
output.append(min(noise[i], noise[i+1]))
return output
for i in range(5):
random.seed(i)
noise = [random.randint(1, 3) for i in range(mapsize)]
print_chart(i, adjacent_min(adjacent_min(noise)))Теперь карты стали ещё более сглаженными и в них ещё меньше гор. Думаю, мы слишком сгладили, потому что горы появляются с холмами не слишком часто. Поэтому наверно лучше вернуться в этом примере на один уровень сглаживания назад.
Это стандартный для процедурного генерирования процесс: вы пробуете что-нибудь, смотрите, выглядит ли это хорошо, если нет, возвращаетесь и пробуете что-нибудь другое.
Примечание: сглаживание в обработке сигналов называется фильтром нижних частот. Иногда он используется для устранения ненужного шума.
Подведём итог:
- Шум — это набор случайных чисел, обычно выстроенный в линию или сетку.
- При процедурном генерировании часто нужно добавить шум для создания вариаций.
- Простой выбор случайных чисел (не важно, однородный или неоднородный) приводит к шуму, в котором каждое число не связано с окружающими его.
- Часто нам нужен шум с определёнными характеристиками, например, получение гор рядом с холмами.
- Существует множество способов создания шума.
- Некоторые функции шума создают шум непосредственно, другие берут существующий шум и модифицируют его.
Подбор функции шума — это часто процесс проб и ошибок. Понимание сущности работы шума и способов его модификации позволяет делать более осмысленный выбор.
3. Создание шума
В предыдущем разделе мы выбирали шум с помощью случайных чисел в качестве выходных данных, а затем сглаживали их. Это стандартный паттерн: начинать с функции шума, использующей в качестве параметров случайные числа. Мы использовали его, когда случайное число выбирало положение сокровища, а затем мы использовали другой, где случайные числа выбирали долины/холмы/горы. Можно модифицировать имеющийся шум, чтобы изменить его форму согласно требованиям. Мы модифицировали функцию шума долин/холмов/гор, сгладив её. Есть множество разных способов модификации функций шума.
Примеры простых генераторов 1D/2D-шума:
- Использовать случайные числа напрямую для вывода. Так мы поступили для долин/холмов/гор.
- Использовать случайные числа в качестве параметров для синусов и косинусов, которые используются для вывода.
- Использовать случайные числа как параметры для градиентов, которые используются для вывода. Этот принцип используется в шуме Перлина.
Вот некоторые стандартные способы модификации шума:
- Применить фильтр для уменьшения или усиления определённых характеристик. Для долин/холмов/гор мы использовали сглаживание для уменьшения скачков, увеличения областей долин и создания гор рядом с холмами.
- Добавить несколько функций шума одновременно, обычно со взвешенной суммой, чтобы можно было управлять влиянием каждой функции шума на конечный результат.
- Интерполировать между значениями шума, полученными функцией шума, для генерирования сглаженных областей.
Существует очень много способов создания шума!
В какой-то степени неважно, как был создан шум. Это интересно, но при использовании в игре нужно сосредоточиться на двух аспектах:
- Как вы будете использовать шум?
- Какие свойства вам требуются от функции шума в каждом конкретном случае?
4. Способы использования шума
Самый прямолинейный способ использования функции шума — использовать его напрямую как высоту. В примере выше я сгенерировал долины/холмы/горы, вызывая
random(1,3) в каждой точке карты. Значение шума напрямую используется как высота.Использование шума смещения средней точки (midpoint displacement noise) или шума Перлина — тоже примеры непосредственного использования.
Другой способ использования шума — использовать его как смещение от предыдущего значения. Например, если функция шума возвращает
[2, -1, 5], то можно принять, что первая позиция равна 2, вторая равна 2 + -1 = 1, а третья равна 1 + 5 = 6. См. также «случайное блуждание». Можно сделать обратное, и использовать разность между значениями шума. Это тоже можно воспринимать как модификацию функции шума.Вместо использования шума для задания высот, можно использовать его для аудио.
Или для создания форм. Например, можно использовать шум как радиус графика в полярных координатах. Можно преобразовать функцию 1D-шума, например эту в полярную форму, использовав выходные данные как радиус, а не высоту. Здесь показано, как та же функция выглядит в полярном виде.
Или можно использовать шум как графическую текстуру. Шум Перлина часто используется с этой целью.
Можно применять шум для выбора местоположений объектов, например, деревьев, золотых рудников, вулканов или трещин от землетрясений. В примере выше я использовал случайное число для выбора местоположения сундука с сокровищами.
Также можно использовать шум как пороговую функцию. Например, можно принять, что в любой момент, когда значение выше 3, происходит одно событие, иначе происходит что-то другое. Один из примеров этого — использование 3D-шума Перлина для генерирования пещер. Можно принять, что всё выше определённого порога плотности, а всё ниже этого порога — открытый воздух (пещера).
В моём генераторе полигональных карт я применял различные способы использования шума, но ни в одном из них шум не использовался напрямую для определения высоты:
- Структура графа проще всего, когда используется сетка квадратов или шестиугольников (на самом деле я начал с сетки шестиугольников). Каждый элемент сетки — это полигон. Я хотел добавить в сетку случайности. Это можно сделать, перемещая точки случайным образом. Но мне нужно было что-то более случайное. Я использовал генератор синего шума для размещения полигонов и диаграмму Вороного для из реконструирования. На это ушло бы намного больше времени, но, к счастью, у меня была библиотека (
as3delaunay), которая всё сделала за меня. Но я начал с сетки, что намного проще, и именно с неё я и рекомендую начинать вам. - Береговая линия — это способ отделить сушу от воды. Я использовал два разных способа для её генерирования с помощью этого шума, но можно также попросить дизайнера нарисовать форму самому, и я продемонстрировал это с помощью квадратных и округлых форм. Радиальная форма береговой линии — это функция шума, использующая синусы и косинусы, отрисовывающая их в полярной форме. Форма береговой линии Перлина — это генератор шума, использующий шум Перлина и радиальный возврат в качестве порога. Здесь можно использовать любое количество функций шума.
- Истоки рек располагаются случайным образом.
- Границы между полигонами сменяются с прямых линий на зашумлённые линии. Это похоже на midpoint displacement, но я отмасштабировал их, чтобы они умещались в границы полигонов. Это чисто графический эффект, поэтому код находится в GUI (
mapgen.as) вместо базового алгоритма (Map.as).
В большинстве руководств шум используется довольно прямолинейно, но существует гораздо больше разных способов его использования.
5. Частота шума
Частота — это самое важное свойство, которое нам интересно. Простейший способ понять её — посмотреть на синусоиды. Вот синусоида с низкой частотой, после неё идёт синусоида со средней частотой, а в конце расположена синусоида с высокой частотой:
print_chart(0, [math.sin(i*0.293) for i in range(mapsize)])print_chart(0, [math.sin(i*0.511) for i in range(mapsize)])print_chart(0, [math.sin(i*1.57) for i in range(mapsize)])Как видите, низкие частоты создают широкие холмы, а высокие — более узкие. Частота описывает горизонтальный размер графика; амплитуда описывает вертикальный размер. Помните, ранее я говорил, что карты долин/холмов/гор выглядят «слишком случайными» и хотел создать более широкие области долин или гор? В сущности, мне нужна была низкая частота вариаций.
Если у вас есть непрерывная функция, например,
sin, которая создаёт шум, то увеличение частоты означает умножение входных данных на какой-нибудь коэффициент: sin(2*x) увеличит вдвое частоту sin(x). Увеличение амплитуды означает умножение выходных данных на коэффициент: 2*sin(x) увеличит вдвое амплитуду sin(x). В коде выше видно, что я изменил частоту, умножив входные данные на разные числа. Мы используем амплитуду в следующем разделе, при суммировании нескольких синусоид.Изменение частоты

Изменение амплитуды

Всё вышесказанное относится к 1D, но то же самое происходит и в 2D. Посмотрите на рисунок 1 на этой странице. Вы видите примеры 2D-шума с большой длиной волны (низкой частотой) и малой длиной волны (высокой частотой).Заметьте, что чем выше частота, тем меньше отдельные фрагменты.
Когда говорят о частоте, длине волн или октавах функций шума, имеется в виду именно это, даже если синусоиды не используются.
Кстати о синусоидах, можно делать забавные вещи, сочетая их странными способами. Например, вот низкие частоты слева и высокие частоты справа:
print_chart(0, [math.sin(0.2 + (i * 0.08) * math.cos(0.4 + i*0.3))
for i in range(mapsize)])Обычно одновременно у вас будет множество частот, и правильных ответов о выборе нужной вам никто не даст. Спросите себя: какие частоты мне нужны? Разумеется, ответ зависит от того, как вы планируете их использовать.
6. Цвета шума
«Цвет» шума определяет типы частот, которые в нём содержатся.
На белый шум все частоты влияют одинаково. Мы уже работали с белым шумом, когда выбирали из 1, 2 и 3 для обозначения долин, холмов и гор. Вот 8 последовательностей белого шума:
for i in range(8):
random.seed(i)
print_chart(i, [random.uniform(-1, +1)
for i in range(mapsize)])В красном шуме (также называемом броуновским) больше выделяются низкие частоты (имеют высокие амплитуды). Это значит, что в выходных данных будут более долгие холмы и долины. Генерировать красный шум можно усреднением соседних значений белого шума. Вот те же самые 8 примеров белого шума, но подвергнутые процессу усреднения:
def smoother(noise):
output = []
for i in range(len(noise) - 1):
output.append(0.5 * (noise[i] + noise[i+1]))
return output
for i in range(8):
random.seed(i)
noise = [random.uniform(-1, +1) for i in range(mapsize)]
print_chart(i, smoother(noise))Если внимательно посмотреть на любой из этих восьми примеров, можно заметить, что они сглаженней соответствующего белого шума. Интервалы больших или малых значений более долгие.
Розовый шум находится между белым и красным. Он часто возникает в природе, и обычно подходит для ландшафтов: большие холмы и долины, плюс небольшая рельефность по ландшафту.
С другой части спектра находится фиолетовый шум. В нём более заметны высокие частоты. Фиолетовый шум можно сгенерировать, взяв разность соседних значений белого шума. Вот те же 8 примеров белого шума, подвергнутые процессу вычитания:
def rougher(noise):
output = []
for i in range(len(noise) - 1):
output.append(0.5 * (noise[i] - noise[i+1]))
return output
for i in range(8):
random.seed(i)
noise = [random.uniform(-1, +1) for i in range(mapsize)]
print_chart(i, rougher(noise))Если внимательно посмотреть на любой из восьми примеров, можно заметить, что они грубее соответствующего белого шума. В них меньше долгих интервалов больших/малых значений, и более короткие вариации.
Синий шум находится между фиолетовым и белым. Он часто подходит для расположения объектов: нет ни слишком плотных, ни слишком разреженных областей, приблизительно равномерное распределение по ландшафту. Расположение палочек и колбочек в наших глазах имеет характеристики синего шума. Синий шум может также подойти для отличного вида города. В Википедии есть страница, на которой можно послушать разные цвета шумов.
Мы узнали, как генерировать белый, красный и фиолетовый шум. Но наиболее полезными функциями шума для нас будут белый, розовый и синий. Позже мы попробуем сгенерировать розовый и синий шумы.
Подведём итог:
- Частота — это свойство повторяющихся сигналов, например, синусоид, но мы можем применять её и для шумов.
- Белый шум — самый простой. Он содержит все частоты. Это однородно выбираемые случайные числа.
- Красный, розовый, синий и фиолетовый — другие цвета шумов, которые можно использовать для процедурного генерирования.
- Белый шум можно превратить в красный усреднением.
- Белый шум можно превратить в фиолетовый вычитанием.
7. Сочетание частот
В предыдущих разделах мы рассмотрели «частоты» шума и различные «цвета» шума. Белый шум означает наличие всех частот. В розовом и красном шуме низкие частоты сильнее высоких. В синем и фиолетовом высокие частоты сильнее низких.
Один из способов генерирования шума с нужными частотными характеристиками — найти способ генерирования шума с определёнными частотами, а затем скомбинировать их вместе. Например, предположим, что у нас есть функция шума
noise, сгенерировавшая шум с определённой частотой freq. Тогда если вам нужно, чтобы частоты 1000 Гц были дважды сильнее частот 2000 Гц, а другие частоты отсутствовали, мы можем использовать noise(1000) + 0.5 * noise(2000).Нужно признать, что теперь
sine выглядит довольно шумно, но ему легко придать частоту, поэтому давайте начнём с этого и посмотрим, как далеко мы сможем продвинуться.def noise(freq):
phase = random.uniform(0, 2*math.pi)
return [math.sin(2*math.pi * freq*x/mapsize + phase)
for x in range(mapsize)]
for i in range(3):
random.seed(i)
print_chart(i, noise(1))Вот и всё. Наш базовый строительный кирпичик — это синусоида, смещённая вбок на случайное значение (называемое фазой). Единственная случайность здесь заключается в том, насколько мы её сместили.
Давайте скомбинируем несколько функций шума вместе. Я хочу скомбинировать 8 функций шума с частотами 1, 2, 4, 8, 16, 32 (в некоторых функциях шума степени двойки называются октавами). Я умножу каждую из этих функций шума на определённый коэффициент (см. массив
amplitudes) и суммирую их. Мне нужен способ вычисления взвешенной суммы:def weighted_sum(amplitudes, noises):
output = [0.0] * mapsize # make an array of length mapsize
for k in range(len(noises)):
for x in range(mapsize):
output[x] += amplitudes[k] * noises[k][x]
return outputТеперь я могу использовать функцию
noise и новую функцию weighted_sum:amplitudes = [0.2, 0.5, 1.0, 0.7, 0.5, 0.4]
frequencies = [1, 2, 4, 8, 16, 32]
for i in range(10):
random.seed(i)
noises = [noise(f) for f in frequencies]
sum_of_noises = weighted_sum(amplitudes, noises)
print_chart(i, sum_of_noises)Даже несмотря на то, что мы начали с синусоид, которые совсем не выглядят шумными, их сочетание выглядит довольно шумным.
А если использовать
[1.0, 0.7, 0.5, 0.3, 0.2, 0.1] в качестве весов? Так используется гораздо больше низких частот и совсем нет высоких:
А если бы я использовал в качестве весов
[0.1, 0.1, 0.2, 0.3, 0.5, 1.0]? Низкие частоты имели бы очень малый вес, а у высоких частот он был бы гораздо большим:
Всё, что мы здесь сделали — это взвешенная сумма функций шума на разных частотах, и это заняло меньше 15 строк кода. Мы можем генерировать широкий диапазон различных стилей шума.
Подведём итог:
- Вместо выбора массива случайных чисел мы выбираем единственное случайное число и используем его для смещения синусоиды влево или вправо.
- Можно создавать шум, взяв взвешенную сумму других функций шума, имеющих разные частоты.
- Можно выбрать характеристики шума, выбрав веса для взвешенной суммы.
8. Генерирование радуги
Теперь, когда мы можем генерировать шум, смешивая вместе шум с разной частотой, давайте снова рассмотрим цвет шума.
Опять зайдём на страницу Википедии о цветах шума. Заметьте, что там указан спектр частот. Он говорит нам об амплитуде каждой частоты, присутствующей в шуме. Белый шум — плоский, розовый и красный наклонены вниз, синий и фиолетовый поднимаются вверх.
Спектр частот соотносится с нашими массивами
frequencies и amplitudes из предыдущего раздела.Ранее мы использовали частоты, являющиеся степенями двойки. Различные типы цветного шума имеют гораздо больше частот, поэтому нам нужем массив побольше. Для этого кода вместо степеней двойки (1, 2, 4, 8, 16, 32) я собираюсь использовать все целые частоты от 1 до 30. Вместо записи амплитуд вручную, я напишу функцию
amplitude(f), возвращающую амплитуду любой заданной частоты и создающую по этим данным массив amplitudes.Мы снова можем использовать функции
weighted_sum и noise, но теперь вместо небольшого набора частот у нас будет более длинный массив:frequencies = range(1, 31) # [1, 2, ..., 30]
def random_ift(rows, amplitude):
for i in range(rows):
random.seed(i)
amplitudes = [amplitude(f) for f in frequencies]
noises = [noise(f) for f in frequencies]
sum_of_noises = weighted_sum(amplitudes, noises)
print_chart(i, sum_of_noises)
random_ift(10, lambda f: 1)В этом коде функция
amplitude определяет форму. Если она всегда возвращает 1, то мы получим белый шум. Как же сгенерировать другие цвета шума? Я использую то же случайное начальное число (random seed), но применю для него другую функцию амплитуды:8.1. Красный шум
random_ift(5, lambda f: 1/f/f)8.2. Розовый шум
random_ift(5, lambda f: 1/f)8.3. Белый шум
random_ift(5, lambda f: 1)8.4. Синий шум
random_ift(5, lambda f: f)8.5. Фиолетовый шум
random_ift(5, lambda f: f*f)8.6. Цвета шума
Итак, это довольно удобно. Можно изменять показатель степени функции амплитуды для получения простых форм.
- Красный шум — это f^-2
- Розовый шум — это f^-1
- Белый шум — это f^0
- Синий шум — это f^+1
- Фиолетовый шум — это f^+2
Попробуйте менять показатель степени [в оригинале статьи], чтобы увидеть, как шум из разделов 8.1-8.5 генерируется из одной базовой функции.
Подведём итог:
- Можно генерировать шум взвешенной суммой синусоид с различными частотами.
- Разные цвета шума имеют веса (амплитуды), соответствующие функции f^c.
- Изменяя показатель степени, из одного набора случайных чисел можно получать разные цвета шума.
9. Другие формы шума
Для генерирования разных цветов шума мы заставили амплитуды следовать простым степенным функциям с разными показателями степени. Но мы не ограничены только этими формами. Это самый простой паттерн, отображающийся на логарифмическом графике прямыми линиями. Возможно, существуют другие наборы частот, создающие интересные паттерны для наших нужд. Можно использовать массив амплитуд и настроить их как угодно вместо использования одной функции. Это стоит исследовать, но я пока не занимался этим.
То, что мы делали в предыдущем разделе, можно воспринимать как ряды Фурье. Основная мысль заключается в том, что любую непрерывную функцию можно представить как взвешенную сумму синусоид и косинусоид. В зависимости от выбранных весов меняется внешний вид окончательной функции. Преобразование Фурье связывает исходную функцию с её частотами. Обычно мы начинаем с исходных данных и получаем из них частоты/амплитуды. Это видно в музыкальных проигрывателях, показывающих «спектр» шума.
Прямое направление позволяет анализировать данные и получить частоты; обратное направление позволяет синтезировать данные из частот. В работе с шумом мы обычно занимаемся синтезом. Фактически, мы уже это делали. В предыдущем разделе мы выбрали частоты и амплитуды и сгенерировали шум.
Преобование Фурье имеет множество применений.
На этой странице есть объяснение того, как работает преобразование Фурье. Диаграммы на этой странице интерактивны — можно ввести силу каждой частоты, и страница покажет, как они комбинируются. Комбинируя синусоиды, можно получить множество интересных форм. Например, попробуйте ввести в поле Cycles input
0 -1 0.5 -0.3 0.25 -0.2 0.16 -0.14 и снять флажок Parts. Правда, похоже на гору? В приложении (Appendix) этой страницы есть версия, показывающая, как выглядят синусоиды в полярных координатах.Один из примеров использования преобразования Фурье для генерирования карт см. в технике генерирования ландшафтов синтезом частот Пола Бёрка (Paul Bourke), которая сначала генерирует двухмерный белый шум, затем преобразует его в частоты с помощью преобразования Фурье, затем придаёт ему форму розового шума, а потом преобразует обратно с помощью обратного преобразования Фурье.
Мой небольшой опыт экспериментов с 2D показывает, что в нём всё не так прямолинейно, как в 1D. Если вы хотите посмотреть на мои незавершённые эксперименты, прокрутите к концу этой страницы и подвигайте ползунки.
10. Другие функции шума
В этой статье для генерирования шума мы использовали синусоиды. Это довольно просто. Мы берём несколько функций и суммируем их. Даже если исходные функции не выглядят шумными, результат выглядит достаточно хорошо, особенно учитывая, что мы написали всего 15 строк кода.
Я не изучал подробно другие функции шума, но использую их в своих проектах. Думаю, многие из них генерируют розовый шум:
- Полагаю, в midpoint displacement вместо синусоид используется пилообразный сигнал, а потом суммируются всё более и более высокие частоты с всё более и более низкими амплитудами. Думаю, что получается розовый шум. В результате мы видим заметные грани, которые возникают или из-за пилообразного сигнала (не такого сглаженного, как синусоиды), или из-за использования только частот, являющихся степенями двойки. Точно я не знаю.
- Diamond square — это вариация midpoint displacement, которая позволять скрыть грани, получаемые в midpoint displacement.
- Одна октава шума Перлина/симплекс-шума генерирует сглаженный шум с определённой частотой. Чтобы сделать шум розовым, обычно суммируются несколько октав шума Перлина.
- Мне кажется, что фрактальное броуновское движение (ФБД) тоже генерирует розовый шум суммированием нескольких функций шума.
- Алгоритм Восса-Маккартни выглядит похожим на midpoint displacement. Он суммирует несколько функций белого шума с разными частотами.
- Генерировать розовый шум напрямую можно вычислением обратного преобразования Фурье для нужных частот. Именно это делает пример в предыдущем разделе. Пол Бёрк (Paul Bourke) описывает его как синтез частот (Frequency Synthesis) и демонстрирует как оно выглядит для 2D-шума, генерирующего трёхмерные карты высот.
Некоторые сведения об алгоритме Восса-Маккартни заставляют меня думать, что суммирование шума с разными частотами не совсем является розовым шумом, но достаточно близко к нему для генерирования карт. Стыки, получаемые в midpoint displacement, скорее всего, получаются из-за него, или может быть из-за функции интерполяции, точно я не знаю.
Я нашёл не так много способов генерирования синего шума.
- Для моего проекта генератора карт я использовал алгоритм Ллойда с диаграммами Вороного, чтобы сгенерировать нужный мне синий шум. У меня уже была библиотека, создающая диаграммы Вороного, поэтому было проще снова использовать её, чем реализовывать как отдельный этап.
- Ещё один способ генерирования синего шума — пятна Пуассона. Если в вашем проекте ещё не используется библиотека Вороного, то пятно Пуассона выглядит проще. См. также эту статью, описывающую использование пятна в играх.
- Рекурсивные плитки Вана тоже могут генерировать синий шум. Я пока ещё не изучал их, но надеюсь взяться за это в будущем.
- Может быть, получится также напрямую генерировать синий шум, вычисляя обратное преобразование Фурье из спектра частот синего шума, но я пока не пробовал.
Я даже не уверен, что для карт мне нужен обязательно правильный синий шум, но это описывается в литературе как синий шум. Синий шум, который я генерирую с помощью синусоид, похож на то, что мне нужно, но перечисленные выше техники, как мне кажется, должны лучше подходить для игр.
11. Дополнительное чтение
Эта статья изначально была заметками для себя. При публикации я усовершенствовал диаграммы и добавил пару интерактивных. Я потратил на неё гораздо меньше времени, чем на другие свои статьи, но я экспериментировал с объяснением некоторых тем, надеясь, что это позволит мне охватить больше информации.
Также у меня есть эксперименты с 2D, которые не настолько отполированы, как данные этой статьи. В том числе там есть 3D-визуализация двухмерной карты высот.
Другие темы, в которые я не сильно вдавался:
- На странице libnoise есть фантастическое объяснение функций шума и интерполяций, в том числе объяснение того, почему функция интерполяции должна иметь плавные производные
- В этом введении в шум Перлина объясняются теория, стоящая за шумом Перлина, и связанные с ним функции шума
- В ещё одном введении в шум Перлина также описывается теория
- В этом введении в двухмерное преобразование Фурье есть куча отличных изображений, которые помогут в интуитивном понимании пространства частот
- green_meklar на reddit рассказывает о способах комбинирования и искажения шума для генерирования ландшафтов
- В Math/StackExchange есть описания преобразования Фурье
- Как создавать одномерный и двухмерный шум
- Заметки Стефана Густавсона (Stefan Gustavson) о шуме Перлина, в том числе о том, как делать его бесшовным, и о том, почему иногда стоит предпочесть вместо него симплекс-шум
- Страница из книги, описывающей ФБД
- На этой и этой страницах объясняется принцип работы быстрого преобразования Фурье
- Использование нелинейных функций интерполяции
- Винеровский процесс
- Броуновский мост в Википедии
- Более математические заметки Джулиуса Смита (Julius Smith) о преобразовании Фурье, в особенности для работы с аудио
- Шум для процедурного генерирования планет
- Генерирование ландшафта с холмами вместо синусоид
- Генерирование шума в графическом процессоре
- Заметки Notch'а о генерировании ландшафта Minecraft — изначально он использовал и двухмерный шум Перлина для высот, и трёхмерный шум Перлина для порога плотности, но сейчас использует двухмерную карту высот, а пещеры генерирует с помощью червей Перлина
- Генерирование процедурного 3D-мира
- Создание бесшовных функций 2D-шума — для создания бесшовного 2D-шума вместо функций смешивания 2D-шума используется 4D-шум