Недавно в институте я столкнулся с любопытной криптографической задачей, которой хотел бы поделиться с Сообществом. Одним предложением задачу могу обозначить, как "Атака на LSX-шифр, не содержащий нелинейной компоненты, на основе открытых текстов". Так как русскоязычных примеров решения таких учебных «головоломок» встречается немного, а сама задача рекомендована для начинающих свой путь специалистов, я считаю, что такая статья может быть интересна юному криптоаналитику. Пожалуйте под кат.

Байтовая подстановка шифра AES-256 определяется некоторой последовательностью операций в поле
шифра AES-256 определяется некоторой последовательностью операций в поле  и также может быть задана массивом из 256 байт:
и также может быть задана массивом из 256 байт:
Определим модифицированный вариант шифра – «AES-256-М», который будет отличаться от оригинального только подстановкой, а именно:
Задача. Имеется шифртекст длиной 5120 бит (40 блоков), который был получен шифрованием открытого текста шифром «AES-256-М» в режиме простой замены на неизвестном ключе. Известен первый блок открытого текста. Предложить осуществимый на практике способ вскрытия неизвестной части шифртекста.
Рассмотрим общую структуру LSX-шифров, одним из представителей которых является AES Rijndael.
В основе шифров LSX-архитектуры лежит итеративное применение раундовой функции к блоку a преобразуемого текста (длина блока a для большинства современных шифров – 128 бит).
Раундовая функция состоит из трех преобразований:
 — сложение по модулю 2 входного блока с итерационным ключом
— сложение по модулю 2 входного блока с итерационным ключом  (
( , где
, где  – число раундов шифра);
– число раундов шифра);
 — применение фиксированной подстановки
— применение фиксированной подстановки  к каждому байту блока;
к каждому байту блока;
 — линейное преобразование.
— линейное преобразование.
Схематично LSX-преобразование можно представить как
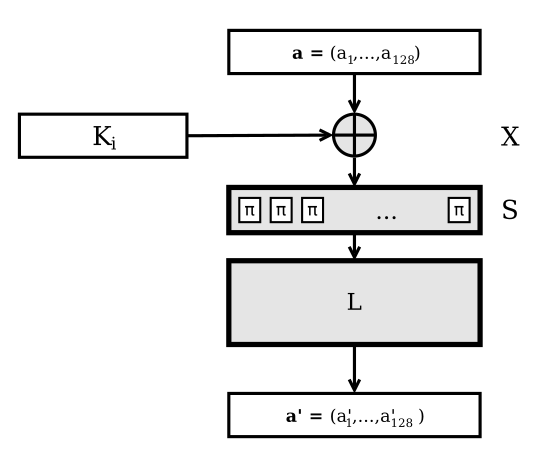
В каждом раунде LSX-шифра используется отдельный раундовый ключ некоторым образом формируемый из первичного ключа
некоторым образом формируемый из первичного ключа  . Битовая длина первичного ключа
. Битовая длина первичного ключа  обычно равна длине итерационного ключа или превосходит её. Процедуры ключевой развертки итерационных ключей из первичного существенным образом отличаются у различных шифров.
обычно равна длине итерационного ключа или превосходит её. Процедуры ключевой развертки итерационных ключей из первичного существенным образом отличаются у различных шифров.
Общая формула шифрующего преобразования для LSX-шифра с числом раундов, равным
для LSX-шифра с числом раундов, равным  , может быть записана в следующем виде:
, может быть записана в следующем виде:
Схематично общую структуру LSX-шифра можно представить как
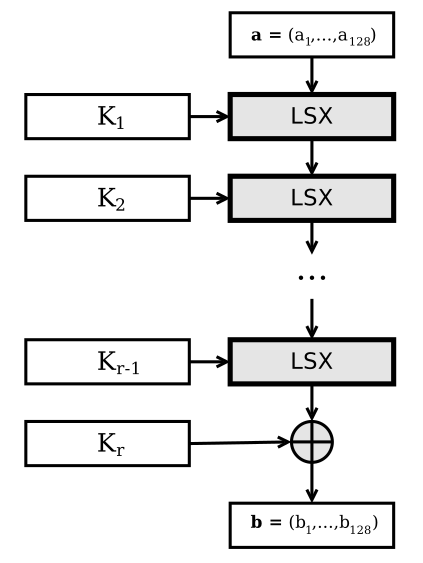
Процесс расшифрования выполняется с помощью обратных преобразований:
 — сложение по модулю 2 входного блока с итерационным ключом;
— сложение по модулю 2 входного блока с итерационным ключом;
 — применение обратной к
— применение обратной к  подстановки;
подстановки;
 — применение обратного
— применение обратного  -преобразования (
-преобразования ( – единичная подстановка).
– единичная подстановка).
Формула для расшифрования
 -раундового LSX-шифра:
-раундового LSX-шифра:
В шифрах LSX-архитектуры огромную роль играют подстановки – биективные отображения вида , где
, где  . Неудачно выбранная подстановка может привести к снижению стойкости всего шифра, а в худшем случае к применимой на практике атаке на шифр.
. Неудачно выбранная подстановка может привести к снижению стойкости всего шифра, а в худшем случае к применимой на практике атаке на шифр.
Не буду поэтапно разбирать сам алгоритм AES, на этом ресурсе это делали уже не один раз: например, можно почитать такие замечательные статьи как эта, вот эта, и, конечно, официальную документацию шифра.
Я постараюсь воспроизвести ход решения данной задачи с точки зрения малоопытного криптографа (самого себя), чтобы показать логику размышлений в случае, когда абсолютно не знаешь, за что браться в первую очередь.
Очевидно, что ключевая особенность этой задачи – это уязвимая подстановка (S-box), поэтому мое исследование проблемы началось с построения таблицы дифференциальных характеристик. Несмотря на то, что классический дифференциальный метод является непрактичным по отношению к AES-like шифрам (число раундов слишком велико), некоторую полезную информацию о модифицированном S-box'е можно попытаться извлечь.
Итак, строим таблицу:
Ине удивляемся результату: оказывается, таблица имеет вырожденный вид – в каждой ее строке есть запись с вероятностью 256/256 (остальные записи соответственно равны 0).
Далее выдвигается предположение, что такой вид дифф. таблица модифицированной подстановки имеет в силу особенностей построения, т. е. она генерирована искусственно. В таком случае было бы неплохо найти возможный способ генерации таких подстановок.
Из базового курса криптографии известно, что основная роль S-box'а в блочном шифре заключается во внесении нелинейности в криптограмму (другими словами, в максимальном сокрытии статистической связи между открытым текстом и шифртекстом), и раз данный нам S-box является уязвимым местом AES-256-M, можно предположить, что он не выполняет свою целевую функцию. Значит, скорее всего, этот S-box является результатом применения какой-либо линейной функции к диапазону чисел .
.
Экспериментальным методом выясняем, что в роли генератора подстановки выступила простая аффинная функция вида , где
, где
 — двоичная матрица размера 8x8,
— двоичная матрица размера 8x8,
 — двоичный 8-битный вектор-столбец.
— двоичный 8-битный вектор-столбец.
Таким образом, наше предположение оказалось верным: если представить байты подстановки в виде двоичных векторов, то модифицированная подстановка превращается в представленное выше аффинное преобразование с линейной зависимостью между входным и выходным набором бит.
Теперь даже можно написать небольшой скрипт для генерации таких подстановок.
Итак, единственный компонент шифра, который должен был быть нелинейным, оказался очень даже линейным, поэтому нетрудно догадаться, в каком направлении двигаться дальше.
Найдем альтернативное бит-ориентированное представление всех линейных преобразований шифра AES Rijndael такое, чтобы было возможно «встроить» линейную теперь операцию применения подстановки к каждому байту блока в одну большую линейную трансформацию.
Операция SubBytes, как раз представляющая преобразование в LSX-шифре, теперь выглядит как
в LSX-шифре, теперь выглядит как  , где
, где  — шифруемый блок,
— шифруемый блок,  и
и  описаны выше.
описаны выше.
Следовательно, бит-ориентированное представление операции SubBytes пример вид:
 , где
, где
 — 128-битное представление блока
— 128-битное представление блока  ;
;
 ;
; 
Обратимся к [1] для определения матрицы, отвечающей за операцию ShiftRows. Эта матрица имеет следующий вид:
 где
где 
И преобразование ShiftRows принимает вид .
.
Здесь потрудней: необходимо оригинальную MDS-матрицу над полем привести к эквивалентной форме над
привести к эквивалентной форме над  . Для этого вспомним, что алгебраическая структура поля
. Для этого вспомним, что алгебраическая структура поля  вытекает из рассмотрения кольца многочленов (переменной
вытекает из рассмотрения кольца многочленов (переменной  ) с коэффициентами из
) с коэффициентами из  по модулю некоторого многочлена
по модулю некоторого многочлена  степени 8 (a.k.a. фактор кольцо
степени 8 (a.k.a. фактор кольцо ![$GF(2)[x]/f(x)$](https://habrastorage.org/getpro/habr/formulas/baa/bdc/44f/baabdc44fc8fd398ee6049109d9f99b3.svg) ). Для AES'а
). Для AES'а  — неприводимый над
— неприводимый над  полином 8-й степени.
полином 8-й степени.
Далее: любой элемент из представи́м как сумма базисных
представи́м как сумма базисных  . Тогда запомним результаты умножения элемента
. Тогда запомним результаты умножения элемента  на все базисные:
на все базисные:
Так как выполняется дистрибутивность по сложению и умножению, то в совокупности с рассуждениями выше элемент можно представить в виде матрицы с коэффициентами из
можно представить в виде матрицы с коэффициентами из  :
:
Тогда очевидно, что элемент перейдет в единичную матрицу
перейдет в единичную матрицу  , а элемент
, а элемент  перейдет в
перейдет в  .
.
Для проверки наших рассуждений можно заглянуть в [2], где предлагается аналогичная матрица для бит-ориентированного умножения на элемент
для бит-ориентированного умножения на элемент  из
из  .
.
В результате, принимая во внимание то, что во время оригинальной трансформации MixColumns строка MDS-матрицы умножается на столбец состояния state, составим матрицу для бит-ориентированного представления данной трансформации (под спойлером).
для бит-ориентированного представления данной трансформации (под спойлером).
И тогда соответствующее преобразование примет вид .
.
Анализ практически завершен, подготовим все необходимое для атаки.
Рассмотрим один раунд шифра AES-256-M.
В стандартном виде:
В матричном виде над :
:
но так как , то
, то
где — матрица, представляющая весь линейный рассеивающий слой AES-256-M.
— матрица, представляющая весь линейный рассеивающий слой AES-256-M.
Рассмотрим 15 раундов (14 + раунд инициализации ключом) шифра AES-256-M в матричном виде:
Раскроим скобки:
где — условный «мастер-ключ», который можно использовать для дешифрования других блоков (т. к. шифрование проводится в режиме ECB):
— условный «мастер-ключ», который можно использовать для дешифрования других блоков (т. к. шифрование проводится в режиме ECB):
И вот та самая «магическая» формула для дешифровки остальных блоков шифртекста, из-за который мы сегодня собрались:
В оригинальной реализации AES Rijndael операция MixColumns опущена на последнем раунде шифра в силу своей бесполезности на этом этапе. В данном решении это не учитывается (т. е. MixColumns используется и после сложения с последним раундовым ключом) для упрощения демонстрации результата.
Сперва хотелось бы отметить, что матрицу можно легко получить с помощью алгебраического аппарата Sage:
можно легко получить с помощью алгебраического аппарата Sage:
Небольшое программное демо, которое покажет «вживую», как проходит взлом, выложено на Гитхабе.
Что можно сказать о задачах такого рода? Такие задачи являются отличным примером того, как такая, на первый взгляд, несущественная модификация оригинального алгоритма, как «кастомная» подстановка (которая вроде бы даже выглядит псевдослучайной, даже более того – проходит некоторую часть статистических тестов NIST, см. спойлер ниже) может выродить международный стандарт шифрования в тривиальное аффинное преобразование с известной матрицей.
Спасибо за внимание!

Условие
Байтовая подстановка
63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76
ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0
b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15
04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75
09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84
53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf
d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8
51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2
cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73
60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db
e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79
e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08
ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a
70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e
e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df
8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16
Определим модифицированный вариант шифра – «AES-256-М», который будет отличаться от оригинального только подстановкой, а именно:
2b c4 4d a2 76 99 10 ff 56 b9 30 df 0b e4 6d 82
db 34 bd 52 86 69 e0 0f a6 49 c0 2f fb 14 9d 72
95 7a f3 1c c8 27 ae 41 e8 07 8e 61 b5 5a d3 3c
65 8a 03 ec 38 d7 5e b1 18 f7 7e 91 45 aa 23 cc
cb 24 ad 42 96 79 f0 1f b6 59 d0 3f eb 04 8d 62
3b d4 5d b2 66 89 00 ef 46 a9 20 cf 1b f4 7d 92
75 9a 13 fc 28 c7 4e a1 08 e7 6e 81 55 ba 33 dc
85 6a e3 0c d8 37 be 51 f8 17 9e 71 a5 4a c3 2c
6f 80 09 e6 32 dd 54 bb 12 fd 74 9b 4f a0 29 c6
9f 70 f9 16 c2 2d a4 4b e2 0d 84 6b bf 50 d9 36
d1 3e b7 58 8c 63 ea 05 ac 43 ca 25 f1 1e 97 78
21 ce 47 a8 7c 93 1a f5 5c b3 3a d5 01 ee 67 88
8f 60 e9 06 d2 3d b4 5b f2 1d 94 7b af 40 c9 26
7f 90 19 f6 22 cd 44 ab 02 ed 64 8b 5f b0 39 d6
31 de 57 b8 6c 83 0a e5 4c a3 2a c5 11 fe 77 98
c1 2e a7 48 9c 73 fa 15 bc 53 da 35 e1 0e 87 68
Задача. Имеется шифртекст длиной 5120 бит (40 блоков), который был получен шифрованием открытого текста шифром «AES-256-М» в режиме простой замены на неизвестном ключе. Известен первый блок открытого текста. Предложить осуществимый на практике способ вскрытия неизвестной части шифртекста.
Теоретическое введение
Рассмотрим общую структуру LSX-шифров, одним из представителей которых является AES Rijndael.
Структура LSX-шифра
В основе шифров LSX-архитектуры лежит итеративное применение раундовой функции к блоку a преобразуемого текста (длина блока a для большинства современных шифров – 128 бит).
Раундовая функция состоит из трех преобразований:
Схематично LSX-преобразование можно представить как

В каждом раунде LSX-шифра используется отдельный раундовый ключ
Общая формула шифрующего преобразования
Схематично общую структуру LSX-шифра можно представить как

Процесс расшифрования выполняется с помощью обратных преобразований:
Формула для расшифрования
Подстановки в LSX-шифрах
В шифрах LSX-архитектуры огромную роль играют подстановки – биективные отображения вида
Не буду поэтапно разбирать сам алгоритм AES, на этом ресурсе это делали уже не один раз: например, можно почитать такие замечательные статьи как эта, вот эта, и, конечно, официальную документацию шифра.
Решение
Я постараюсь воспроизвести ход решения данной задачи с точки зрения малоопытного криптографа (самого себя), чтобы показать логику размышлений в случае, когда абсолютно не знаешь, за что браться в первую очередь.
Разведка
Очевидно, что ключевая особенность этой задачи – это уязвимая подстановка (S-box), поэтому мое исследование проблемы началось с построения таблицы дифференциальных характеристик. Несмотря на то, что классический дифференциальный метод является непрактичным по отношению к AES-like шифрам (число раундов слишком велико), некоторую полезную информацию о модифицированном S-box'е можно попытаться извлечь.
Итак, строим таблицу:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Usage: python3 dc.py
from itertools import product
def dc(sbox):
length = len(sbox)
diff_table = [[0] * length for _ in range(length)]
for c, d in product( *([list(range(length))]*2) ):
diff_table[c ^ d][sbox[c] ^ sbox[d]] += 1
count_prob = 0
for c, d in product( *([list(range(length))]*2) ):
if diff_table[c][d] == length:
count_prob += 1
print('{} : {} -> {}'.format(diff_table[c][d], c, d))
return count_prob == length
if __name__ == '__main__':
# sboxm = [ <модифицированная_подстановка> ]
print(dc(sboxm))
И
Далее выдвигается предположение, что такой вид дифф. таблица модифицированной подстановки имеет в силу особенностей построения, т. е. она генерирована искусственно. В таком случае было бы неплохо найти возможный способ генерации таких подстановок.
Из базового курса криптографии известно, что основная роль S-box'а в блочном шифре заключается во внесении нелинейности в криптограмму (другими словами, в максимальном сокрытии статистической связи между открытым текстом и шифртекстом), и раз данный нам S-box является уязвимым местом AES-256-M, можно предположить, что он не выполняет свою целевую функцию. Значит, скорее всего, этот S-box является результатом применения какой-либо линейной функции к диапазону чисел
Экспериментальным методом выясняем, что в роли генератора подстановки выступила простая аффинная функция вида
Таким образом, наше предположение оказалось верным: если представить байты подстановки в виде двоичных векторов, то модифицированная подстановка превращается в представленное выше аффинное преобразование с линейной зависимостью между входным и выходным набором бит.
Теперь даже можно написать небольшой скрипт для генерации таких подстановок.
Генерируем вырожденные подстановки длины 2^n
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Usage: python3 generate_affine_sbox.py <sbox_length>
import numpy as np
import random
import math
import sys
from itertools import product
# ----------------------------------------------------------
# ---------------------- AFFINE SBOX -----------------------
# ----------------------------------------------------------
"""
Affine function: y(x) = M*x + v, where
M is 8x8 boolean matrix,
v is 8-bit constant vector column,
* is bitwise AND (&),
+ is bitwise XOR (^).
"""
def affine_function(x, M, v):
Mx = (np.dot(M, x) % 2).T
y = Mx ^ v
return y
def S(x, M, v, bin_length):
raw_value = list(affine_function(to_bin(x, bin_length), M, v).flat)
return int(''.join([ str(b) for b in raw_value ]), 2)
def generate_affine_sbox(length):
bin_length = len(bin(length-1)[2:])
np.random.seed()
while True:
M = np.random.randint(0, 2, size=(bin_length, bin_length))
if np.linalg.det(M).astype(int) % 2:
break
v = np.random.randint(0, 2, size=(1, bin_length))
sbox = [ S(i, M, v, bin_length) for i in range(length) ]
if not any_duplicates(sbox) and is_sbox_degenerate(sbox):
return (sbox, M, v)
return (None, None, None)
# ----------------------------------------------------------
# ----------------------- UTILITIES ------------------------
# ----------------------------------------------------------
def to_bin(number, bin_length):
return np.array([ [int(b)] for b in bin(number)[2:].zfill(bin_length) ])
def print_sbox(name, sbox, length):
dim = math.sqrt(length)
print('{} = {{'.format(name), end='')
if dim.is_integer():
print('\n\t', end='')
for i in range(length):
if not (i % dim) and i:
print('\n\t', end='')
print('{: >5}'.format(sbox[i]), end=', ')
print('.\n}')
else:
for item in sbox:
print(item, end=', ')
print('.}')
def any_duplicates(sbox):
seen = set()
for item in sbox:
if item not in seen:
seen.add(item)
else:
return True
return False
def is_sbox_degenerate(sbox):
length = len(sbox)
diff_table = [[0] * length for _ in range(length)]
for c, d in product( *([list(range(length))]*2) ):
diff_table[c ^ d][sbox[c] ^ sbox[d]] += 1
count_prob = 0
for c, d in product( *([list(range(length))]*2) ):
if diff_table[c][d] == length:
count_prob += 1
#print('{} : {} -> {}'.format(diff_table[c][d], c, d))
return count_prob == length
# ----------------------------------------------------------
# -------------------------- MAIN --------------------------
# ----------------------------------------------------------
if __name__ == '__main__':
if len(sys.argv) != 2:
print('Usage: python3 {} <sbox_length>'.format(sys.argv[0]))
sys.exit(1)
try:
length = int(sys.argv[1])
except ValueError:
print("Invalid input type")
sys.exit(1)
if length & (length-1) != 0 or length < 1:
print("Sbox length must be a power of two and > 1")
sys.exit(1)
while True:
sbox, M, v = generate_affine_sbox(length)
if sbox:
print('M = \n{}\n'.format(repr(M)))
print('v = \n{}\n'.format(repr(v)))
print_sbox('Affine Sbox', sbox, length)
break
Подготовка к атаке
Итак, единственный компонент шифра, который должен был быть нелинейным, оказался очень даже линейным, поэтому нетрудно догадаться, в каком направлении двигаться дальше.
Найдем альтернативное бит-ориентированное представление всех линейных преобразований шифра AES Rijndael такое, чтобы было возможно «встроить» линейную теперь операцию применения подстановки к каждому байту блока в одну большую линейную трансформацию.
SubBytes
Операция SubBytes, как раз представляющая преобразование
Следовательно, бит-ориентированное представление операции SubBytes пример вид:
ShiftRows
Обратимся к [1] для определения матрицы, отвечающей за операцию ShiftRows. Эта матрица имеет следующий вид:
И преобразование ShiftRows принимает вид
MixColumns
Здесь потрудней: необходимо оригинальную MDS-матрицу над полем
Далее: любой элемент из
Так как выполняется дистрибутивность по сложению и умножению, то в совокупности с рассуждениями выше элемент
Тогда очевидно, что элемент
Для проверки наших рассуждений можно заглянуть в [2], где предлагается аналогичная матрица
В результате, принимая во внимание то, что во время оригинальной трансформации MixColumns строка MDS-матрицы умножается на столбец состояния state, составим матрицу
MC
( C2 00 00 00 C3 00 00 00 C1 00 00 00 C1 00 00 00 )
( 00 C2 00 00 00 C3 00 00 00 C1 00 00 00 C1 00 00 )
( 00 00 C2 00 00 00 C3 00 00 00 C1 00 00 00 C1 00 )
( 00 00 00 C2 00 00 00 C3 00 00 00 C1 00 00 00 C1 )
( C1 00 00 00 C2 00 00 00 C3 00 00 00 C1 00 00 00 )
( 00 C1 00 00 00 C2 00 00 00 C3 00 00 00 C1 00 00 )
( 00 00 C1 00 00 00 C2 00 00 00 C3 00 00 00 C1 00 )
( 00 00 00 C1 00 00 00 C2 00 00 00 C3 00 00 00 C1 )
( C1 00 00 00 C1 00 00 00 C2 00 00 00 C3 00 00 00 )
( 00 C1 00 00 00 C1 00 00 00 C2 00 00 00 C3 00 00 )
( 00 00 C1 00 00 00 C1 00 00 00 C2 00 00 00 C3 00 )
( 00 00 00 C1 00 00 00 C1 00 00 00 C2 00 00 00 C3 )
( C3 00 00 00 C1 00 00 00 C1 00 00 00 C2 00 00 00 )
( 00 C3 00 00 00 C1 00 00 00 C1 00 00 00 C2 00 00 )
( 00 00 C3 00 00 00 C1 00 00 00 C1 00 00 00 C2 00 )
( 00 00 00 C3 00 00 00 C1 00 00 00 C1 00 00 00 C2 )
И тогда соответствующее преобразование примет вид
Атака
Анализ практически завершен, подготовим все необходимое для атаки.
Один раунд
Рассмотрим один раунд шифра AES-256-M.
В стандартном виде:
В матричном виде над
но так как
где
Несколько раундов
Рассмотрим 15 раундов (14 + раунд инициализации ключом) шифра AES-256-M в матричном виде:
Раскроим скобки:
где
И вот та самая «магическая» формула для дешифровки остальных блоков шифртекста, из-за который мы сегодня собрались:
Примечание
В оригинальной реализации AES Rijndael операция MixColumns опущена на последнем раунде шифра в силу своей бесполезности на этом этапе. В данном решении это не учитывается (т. е. MixColumns используется и после сложения с последним раундовым ключом) для упрощения демонстрации результата.
Заключение, код, литература
Сперва хотелось бы отметить, что матрицу
Как это сделать
sage: L = matrix(ZZ, [ <наша_матрица_L> ]).base_extend(GF(2))
sage: invL = L.inverse()
sage: invL14 = invL^(14)
sage: invL14.str()
Исходный код
Небольшое программное демо, которое покажет «вживую», как проходит взлом, выложено на Гитхабе.
Вывод
Что можно сказать о задачах такого рода? Такие задачи являются отличным примером того, как такая, на первый взгляд, несущественная модификация оригинального алгоритма, как «кастомная» подстановка (которая вроде бы даже выглядит псевдослучайной, даже более того – проходит некоторую часть статистических тестов NIST, см. спойлер ниже) может выродить международный стандарт шифрования в тривиальное аффинное преобразование с известной матрицей.
NIST Statistical Test Suite
Изменённая подстановка прошла:
- Monobit Frequency Test;
- Block Frequency Test;
- Runs Test;
- Serial Test;
- Approximate Entropy Test;
- Cumulative Sums Test.
Спасибо за внимание!
Список литературы
- Algebraic Aspects of the Advanced Encryption Standard by Carlos Cid, Sean Murphy, Matthew Robshaw
- Advances in Cryptology — CRYPTO 2015 – 35th Annual Cryptology Conference, Santa Barbara, CA, USA, August 16-20, 2015, Proceedings, Part 1