
Первая часть статьи может быть доказательством того, что трассировщики лучей — это изящный пример программного обеспечения, позволяющий создавать потрясающе красивые изображения исключительно с помощью простых и интуитивно понятных алгоритмов.
К сожалению, эта простота имеет свою цену: низкую производительность. Несмотря на то, что существует множество способов оптимизации и параллелизации трассировщиков лучей, они всё равно остаются слишком затратными с точки зрения вычислений для выполнения в реальном времени; и хотя оборудование продолжает развиваться и становится быстрее с каждым годом, в некоторых областях применения необходимы красивые, но в сотни раз быстрее создаваемые изображения уже сегодня. Из всех этих областей применения самыми требовательными являются игры: мы ожидаем рендеринга отличной картинки с частотой не менее 60 кадров в секунду. Трассировщики лучей просто с этим не справятся.
Тогда как это удаётся играм?
Ответ заключается в использовании совершенно иного семейства алгоритмов, которое мы исследуем во второй части статьи. В отличие от трассировки лучей, которая получалась из простых геометрических моделей формирования изображений в человеческом глазе или в камере, сейчас мы будем начинать с другого конца — зададимся вопросом, что мы можем отрисовать на экране, и как отрисовать это как можно быстрее. В результате мы получим совершенно другие алгоритмы, которые создают примерно похожие результаты.
Прямые
Снова начнём с нуля: у нас есть холст с размерами
Допустим, у нас есть две точки,
Давайте начнём с представления прямой с параметрическими координатами, как мы делали это ранее с лучами (эти «лучи» — не что иное, как прямые в 3D). Любую точку на прямой можно получить, начав с
Мы можем разложить это уравнение на два, по одному для каждой из координат:
Давайте возьмём первое уравнение и вычислим
Теперь мы можем подставить это выражение во второе уравнение вместо
Немного преобразуем его:
Заметьте, что
Что же такое
Давайте вернёмся к уравнению. Раскроем скобки:
Группируем константы:
Выражение
Это классическая линейная функция, которой можно представить почти все прямые. Ею нельзя описать вертикальные прямые, потому что они имеют бесконечное количество значений
Итак, теперь у нас есть способ вычисления значения
DrawLine(P0, P1, color) {
a = (y1 - y0)/(x1 - x0)
b = y0 - a*x0
for x = x0 to x1 {
y = a*x + b
canvas.PutPixel(x, y, color)
}
}В этом фрагменте
x0 и y0 — это координаты P0; в дальнейшем я буду использовать эту удобную запись. Также заметьте, что оператор деления / должен выполнять не целочисленное деление, а деление вещественных чисел.Эта функция является непосредственной наивной интерпретацией приведённого выше уравнения, поэтому очевидно, что она работает; но можем ли мы ускорить её работу?
Заметьте, что мы не вычисляем значения
Мы можем воспользоваться этим для создания более быстрого алгоритма. Давайте возьмём разность между
Это не очень удивительно; в конце концов, наклон
Интересно то, что мы можем тривиальным образом получить следующее:
Это значит, что мы можем вычислить следующее значение
Считая, что
DrawLine(P0, P1, color) {
a = (y1 - y0)/(x1 - x0)
y = y0
for x = x0 to x1 {
canvas.PutPixel(x, y, color)
y = y + a
}
}Эта новая версия функции имеет новое ограничение: она может отрисовывать прямые только слева направо, то есть при
P0 и P1, чтобы превратить её в лево-правую версию той же прямой, после чего отрисуем её как раньше:DrawLine(P0, P1, color) {
# Make sure x0 < x1
if x0 > x1 {
swap(P0, P1)
}
a = (y1 - y0)/(x1 - x0)
y = y0
for x = x0 to x1 {
canvas.PutPixel(x, y, color)
y = y + a
}
}Теперь мы можем отрисовать пару прямых. Вот

Вот как она выглядит вблизи:
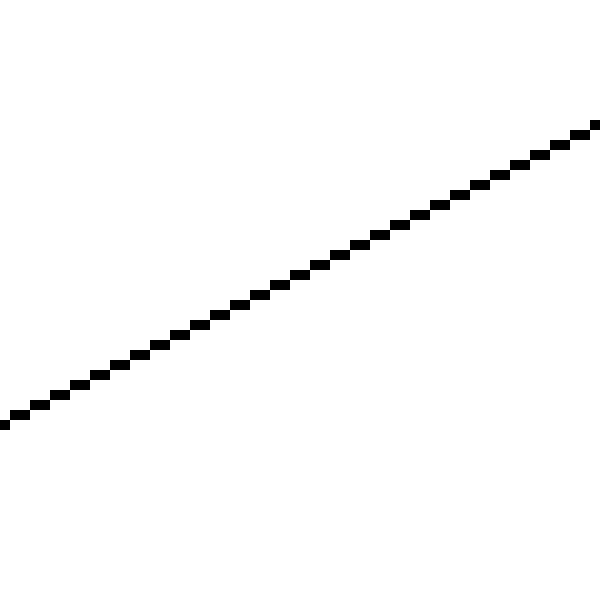
Прямая выглядит ломаной потому, что мы можем рисовать пиксели только по целочисленным координатам, а математические прямые на самом деле имеют нулевую ширину; рисуемое нами является дискретизированным приближением к идеальной прямой
Давайте попробуем нарисовать ещё одну прямую,

А вот как она выглядит вблизи:
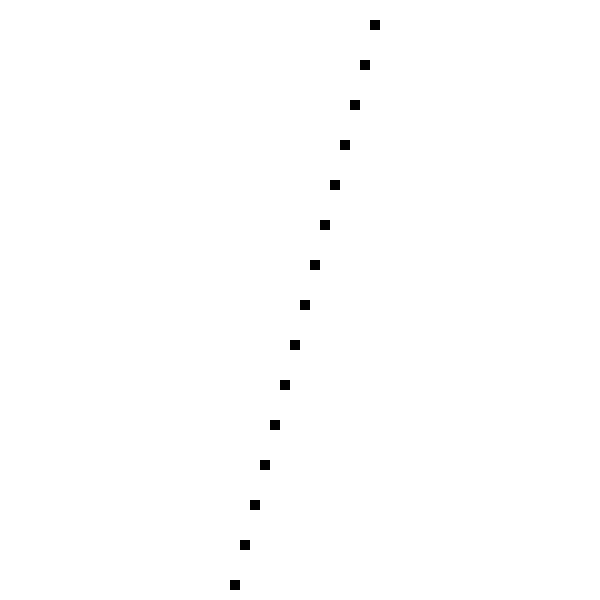
Ой. Что случилось?
Алгоритм работал так, как и задумано; он прошёл слева направо, вычислил значение
Это прямое последствие выбора формулировки, в которой
Мы без всяких проблем можем рисовать горизонтальные прямые. Почему же нам не удаётся так же просто отрисовывать вертикальные линии?
Как оказывается, мы можем это сделать. Выбор
DrawLine(P0, P1, color) {
# Make sure y0 < y1
if y0 > y1 {
swap(P0, P1)
}
a = (x1 - x0)/(y1 - y0)
x = x0
for y = y0 to y1 {
canvas.PutPixel(x, y, color)
x = x + a
}
}Это аналогично предыдущей
DrawLine, за исключением перемены мест вычислений Нам просто нужно выбирать нужную версию функции в зависимости от прямой, которую нужно нарисовать. И критерии будут достаточно простыми; имеет ли прямая более различающиеся значения
Вот версия
DrawLine, обрабатывающая все случаи:DrawLine(P0, P1, color) {
dx = x1 - x0
dy = y1 - y0
if abs(dx) > abs(dy) {
# Прямая ближе к горизонтальной
# Проверяем, что x0 < x1
if x0 > x1 {
swap(P0, P1)
}
a = dy/dx
y = y0
for x = x0 to x1 {
canvas.PutPixel(x, y, color)
y = y + a
}
} else {
# Прямая ближе к вертикальной
# Проверяем, что y0 < y1
if y0 > y1 {
swap(P0, P1)
}
a = dx/dy
x = x0
for y = y0 to y1 {
canvas.PutPixel(x, y, color)
x = x + a
}
}
}Это безусловно сработает, но код не особо красив; в нём есть две реализации кода, инкрементно вычисляющих линейную функцию, и эта логика вычислений и выбора перемешана. Поскольку мы будем часто использовать линейные функции, то стоит потратить немного времени на разделение кода.
У нас есть две функции,
Разумеется, любую функцию можно записать как
Interpolate (i0, d0, i1, d1) {
values = []
a = (d1 - d0) / (i1 - i0)
d = d0
for i = i0 to i1 {
values.append(d)
d = d + a
}
return values
}Заметьте, что значение
values[0], значение для values[1], и так далее; в общем случае, значение values[i_n - i_0], если считать, что Существует тупиковый случай, который нужно учитывать; нам может понадобиться вычислить
Interpolate (i0, d0, i1, d1) {
if i0 == i1 {
return [ d0 ]
}
values = []
a = (d1 - d0) / (i1 - i0)
d = d0
for i = i0 to i1 {
values.append(d)
d = d + a
}
return values
}Теперь мы можем написать
DrawLine с использованием Interpolate:DrawLine(P0, P1, color) {
if abs(x1 - x0) > abs(y1 - y0) {
# Прямая ближе к горизонтальной
# Проверяем, что x0 < x1
if x0 > x1 {
swap(P0, P1)
}
ys = Interpolate(x0, y0, x1, y1)
for x = x0 to x1 {
canvas.PutPixel(x, ys[x - x0], color)
}
} else {
# Прямая ближе к вертикальной
# Проверяем, что y0 < y1
if y0 > y1 {
swap(P0, P1)
}
xs = Interpolate(y0, x0, y1, x1)
for y = y0 to y1 {
canvas.PutPixel(xs[y - y0], y, color)
}
}
}Этот
DrawLine может правильно обрабатывать все случаи:
Исходный код и рабочее демо >>
Хотя эта версия не сильно короче предыдущей, она чётко разделяет вычисление промежуточных значений
Interpolate в последующих главах.Следует учесть, что это не самый лучший или быстрый алгоритм отрисовки; важным результатом этой главы стал
Interpolate, а не DrawLine. Лучшим алгоритмом отрисовки линий скорее всего является алгоритм Брезенхэма.Заполненные треугольники
Мы можем использовать метод
DrawLine для отрисовки контура треугольника. Такой тип контура называется каркасным, потому что он выглядит как каркас треугольника:DrawWireframeTriangle (P0, P1, P2, color) {
DrawLine(P0, P1, color);
DrawLine(P1, P2, color);
DrawLine(P2, P0, color);
}Мы получим вот такой результат:

Можем ли мы залить треугольник каким-нибудь цветом?
Как обычно бывает в компьютерной графике, для этого есть множество способов. Мы будем отрисовывать заполненные треугольники, воспринимая их как набор отрезков горизонтальных прямых, которые, если их отрисовать вместе, выглядят как треугольник. Ниже представлено очень грубое первое приближение того, что мы хотим сделать:
для каждой координаты y горизонтальной прямой, занятой треугольником
вычислить x_left и x_right для этого y
DrawLine(x_left, y, x_right, y)Давайте начнём с части «для каждой координаты y горизонтальной прямой, занятой треугольником». Треугольник задаётся тремя вершинами
if y1 < y0 { swap(P1, P0) }
if y2 < y0 { swap(P2, P0) }
if y2 < y1 { swap(P2, P1) }Затем нам нужно вычислить
x_left и x_right. Это немного сложнее, потому что у треугольника три, а не две стороны. Однако с точки зрения значений x_right получаются или от длинной стороны, или от обеих коротких сторон; а значения x_left получаются от другого множества.Мы начнём с вычисления значений
Interpolate, используя в качестве независимого значения x01 = Interpolate(y0, x0, y1, x1)
x12 = Interpolate(y1, x1, y2, x2)
x02 = Interpolate(y0, x0, y2, x2)x02 будет или x_left, или x_right; другой будет конкатенацией x01 и x12.Заметьте, что в этих двух списках есть повторяющееся значение: значение
x01, и первым значением x12. Нам просто нужно избавиться от одного из них.remove_last(x01)
x012 = x01 + x12Наконец у нас есть
x02 и x012, и нам нужно определить, что из них является x_left и x_right. Для этого надо посмотреть на значения m = x02.length / 2
if x02[m] < x012[m] {
x_left = x02
x_right = x012
} else {
x_left = x012
x_right = x02
}Теперь осталось только отрисовать горизонтальные отрезки. По причинам, которые станут понятны позже, мы не будем использовать для этого
DrawLine; вместо этого мы будем отрисовывать пиксели по отдельности.Вот полная версия
DrawFilledTriangle:DrawFilledTriangle (P0, P1, P2, color) {
# Сортировка точек так, что y0 <= y1 <= y2
if y1 < y0 { swap(P1, P0) }
if y2 < y0 { swap(P2, P0) }
if y2 < y1 { swap(P2, P1) }
# Вычисление координат x рёбер треугольника
x01 = Interpolate(y0, x0, y1, x1)
x12 = Interpolate(y1, x1, y2, x2)
x02 = Interpolate(y0, x0, y2, x2)
# Конкатенация коротких сторон
remove_last(x01)
x012 = x01 + x12
# Определяем, какая из сторон левая и правая
m = x012.length / 2
if x02[m] < x012[m] {
x_left = x02
x_right = x012
} else {
x_left = x012
x_right = x02
}
# Отрисовка горизонтальных отрезков
for y = y0 to y2 {
for x = x_left[y - y0] to x_right[y - y0] {
canvas.PutPixel(x, y, color)
}
}
}Вот результат; для проверки мы вызвали
DrawFilledTriangle, а потом DrawWireframeTriangle с одинаковыми координатами, но разными цветами:
Исходный код и рабочее демо >>
Вы можете заметить, что чёрный контур треугольника не полностью совпадает с зелёной внутренней областью; это особенно заметно в правом нижнем ребре треугольника. Так получилось потому, что DrawLine() вычисляет
Затенённые треугольники
В предыдущей части мы разработали алгоритм для отрисовки треугольника и заливки его цветом. Нашей следующей целью будет отрисовка затенённого треугольника, который похож на залитый градиентом.
Хотя затенённые треугольники выглядят красивее, чем одноцветные, это не является основной целью главы; это просто особое применение техники, которую мы создадим. Наверно, она будет самой важной в этом разделе статьи; почти всё остальное будет построено на её основе.
Но давайте начнём с простого. Вместо заполнения треугольника сплошным цветом, мы хотим заполнить его оттенками цвета. Это будет выглядеть так:

Исходный код и рабочее демо >>
Первый шаг заключается в формальном определении того, что мы хотим отрисовать. Для этого мы назначим каждой вершине вещественное значение
Чтобы получить точный цвет пикселя, имея цвет
Вычисление затенения ребра
Итак, для отрисовки затенённого треугольника нам нужно вычислить значение
Однако на этом этапе мы знаем только значения
Давайте сначала рассмотрим рёбра. Выберем ребро
Если более формально, то у нас есть функция
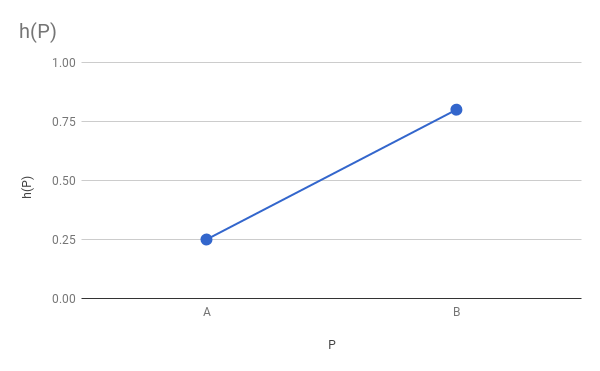
Разумеется, основой кода затенённого треугольника будет код сплошного треугольника, созданный в предыдущей главе. Один их первых шагов включает в себя вычисление конечных точек каждого горизонтального отрезка, то есть
x_left и x_right для сторон Interpolate() для вычисления значений То есть мы можем вычислить промежуточные значения
x01 = Interpolate(y0, x0, y1, x1)
h01 = Interpolate(y0, h0, y1, h1)
x12 = Interpolate(y1, x1, y2, x2)
h12 = Interpolate(y1, h1, y2, h2)
x02 = Interpolate(y0, x0, y2, x2)
h02 = Interpolate(y0, h0, y2, h2)Следующим этапом будет превращение этих трёх векторов в два вектора и определение того, какой из них представляет левосторонние значения, а какой — правосторонние. Заметьте, что значения
x012 имеет значения для правой стороны треугольника, тогда h012 имеет значения для правой стороны треугольника: # Конкатенация коротких сторон
remove_last(x01)
x012 = x01 + x12
remove_last(h01)
h012 = h01 + h12
# Определяем, какая из сторон левая и правая
m = x012.length / 2
if x02[m] < x012[m] {
x_left = x02
x_right = x012
h_left = h02
h_right = h012
} else {
x_left = x012
x_right = x02
h_left = h012
h_right = h02
}Вычисление внутреннего затенения
Остался единственный шаг — отрисовка самих горизонтальных отрезков. Для каждого отрезка мы знаем
Мы снова можем считать, что
Interpolate() для вычисления этих значений:h_segment = Interpolate(x_left[y-y0], h_left[y-y0], x_right[y-y0], h_right[y-y0])И теперь это просто вопрос вычисления цвета для каждого пикселя и его отрисовки.
Вот код вычисления для
DrawShadedTriangle:DrawShadedTriangle (P0, P1, P2, color) {
# Сортировка точек так, что y0 <= y1 <= y2
if y1 < y0 { swap(P1, P0) }
if y2 < y0 { swap(P2, P0) }
if y2 < y1 { swap(P2, P1) }
# Вычисление координат x и значений h для рёбер треугольника
x01 = Interpolate(y0, x0, y1, x1)
h01 = Interpolate(y0, h0, y1, h1)
x12 = Interpolate(y1, x1, y2, x2)
h12 = Interpolate(y1, h1, y2, h2)
x02 = Interpolate(y0, x0, y2, x2)
h02 = Interpolate(y0, h0, y2, h2)
# Конкатенация коротких сторон
remove_last(x01)
x012 = x01 + x12
remove_last(h01)
h012 = h01 + h12
# Определяем, какая из сторон левая и правая
m = x012.length / 2
if x02[m] < x012[m] {
x_left = x02
x_right = x012
h_left = h02
h_right = h012
} else {
x_left = x012
x_right = x02
h_left = h012
h_right = h02
}
# Отрисовка горизонтальных отрезков
for y = y0 to y2 {
x_l = x_left[y - y0]
x_r = x_right[y - y0]
h_segment = Interpolate(x_l, h_left[y - y0], x_r, h_right[y - y0])
for x = x_l to x_r {
shaded_color = color*h_segment[x - xl]
canvas.PutPixel(x, y, shaded_color)
}
}
}Этот алгоритм гораздо более общий, чем может казаться: до момента, в котором
Поэтому этот алгоритм окажется бесценным в последующих частях; не продолжайте чтение, пока не убедитесь, что хорошо поняли его.
Перспективная проекция
На какое-то время мы оставим в покое 2D-треугольники и обратим внимание на 3D; а конкретнее, на то, как можно представить 3D-объекты на 2D-поверхности.
Точно так же, как мы делали в начале части про трассировку лучей, мы начнём с задания камеры. Мы используем те же самые условия: камера находится в
Рассмотрим точку
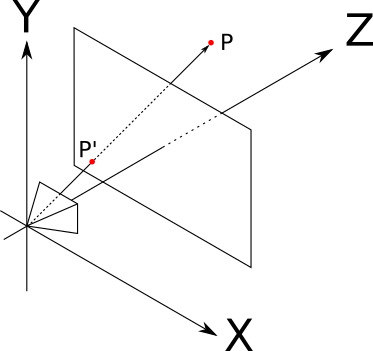
Вот схема ситуации, видимой «справа», то есть когда
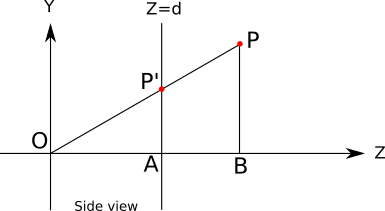
В дополнение к
Понятно, что
Также должно быть понятно, что треугольники
Из него мы получаем
Длина каждого отрезка (со знаком) в этом уравнении — это координата точки, которую мы знаем, или которая нам нужна:
Мы можем нарисовать похожую схему, на этот раз сверху:

Воспользовавшись снова подобными треугольниками, мы получим
Уравнение проецирования
Давайте объединим всё вместе. При задании точки
Самое первое, что нужно здесь сделать — забыть о
Теперь
Наконец мы можем перейти от точки в сцене к пикселю на экране!
Свойства уравнения проецирования
Уравнение проецирования обладает интересными свойствами, о которых стоит поговорить.
Во-первых, в целом оно интуитивно понятно и соответствует опыту реальной жизни. Чем дальше объект вправо (
Однако всё становится менее понятным при уменьшении значения
Ещё одним фундаментальным свойством перспективной проекции является то, что в ней сохраняется принадлежность точек к одной прямой; то есть проекции трёх точек, принадлежащих одной прямой, в окне просмотра тоже будут принадлежать одной прямой (Примечание: это наблюдение может казаться тривиальным, но стоит например заметить, что угол между двумя прямыми не сохраняется; мы видим, как параллельные линии «сходятся» к горизонту, как будто две стороны дороги.). Другими словами, прямая линия всегда выглядит как прямая.
Это имеет для нас очень непосредственную важность: пока мы говорили о проецировании точки, но как насчёт проецировании отрезка прямой или даже треугольника? Благодаря этому свойству проекция отрезка прямой будет отрезком прямой, соединяющимся с проекциями в конечных точках; следовательно, для проецирования полигона достаточно спроецировать его вершины и отрисовать получившийся полигон.
Поэтому мы можем двигаться дальше и отрисовать наш первый 3D-объект: куб. Мы задаём координаты его 8 вершин и отрисовываем линии между проекциями 12 пар вершин, составляющих рёбра куба:
ViewportToCanvas(x, y) {
return (x*Cw/Vw, y*Ch/Vh);
}
ProjectVertex(v) {
return ViewportToCanvas(v.x * d / v.z, v.y * d / v.z)
# Четыре "передних" вершины.
vAf = [-1, 1, 1]
vBf = [1, 1, 1]
vCf = [1, -1, 1]
vDf = [-1, -1, 1]
# Четыре "задних" вершины.
vAb = [-1, 1, 2]
vBb = [1, 1, 2]
vCb = [1, -1, 2]
vDb = [-1, -1, 2]
# Передняя грань.
DrawLine(ProjectVertex(vAf), ProjectVertex(vBf), BLUE);
DrawLine(ProjectVertex(vBf), ProjectVertex(vCf), BLUE);
DrawLine(ProjectVertex(vCf), ProjectVertex(vDf), BLUE);
DrawLine(ProjectVertex(vDf), ProjectVertex(vAf), BLUE);
# Задняя грань.
DrawLine(ProjectVertex(vAb), ProjectVertex(vBb), RED);
DrawLine(ProjectVertex(vBb), ProjectVertex(vCb), RED);
DrawLine(ProjectVertex(vCb), ProjectVertex(vDb), RED);
DrawLine(ProjectVertex(vDb), ProjectVertex(vAb), RED);
# Рёбра, соединяющие переднюю и заднюю грани.
DrawLine(ProjectVertex(vAf), ProjectVertex(vAb), GREEN);
DrawLine(ProjectVertex(vBf), ProjectVertex(vBb), GREEN);
DrawLine(ProjectVertex(vCf), ProjectVertex(vCb), GREEN);
DrawLine(ProjectVertex(vDf), ProjectVertex(vDb), GREEN);И мы получаем нечто подобное:
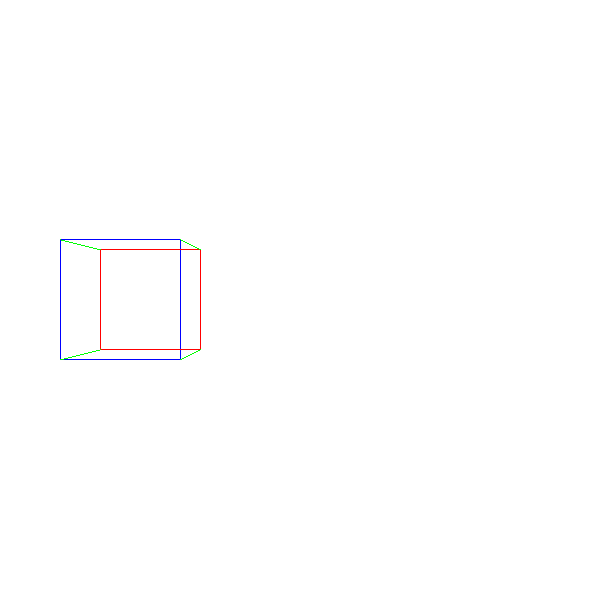
Исходный код и рабочее демо >>
Хотя это и работает, у нас возникли серьёзные проблемы — что если мы хотим отрендерить два куба? Что если мы хотим отрендерить не куб, а что-то другое? Что если мы не знаем, что будем рендерить, пока программа не запущена — например, загружаем 3D-модель с диска? В следующей главе мы узнаем, как решать все эти вопросы.
Настройки сцены
Мы разработали техники для отрисовки треугольника на холсте по заданным координатам его вершин и уравнения для преобразования 3D-координат треугольника в 2D-координаты холста. В этой главе мы узнаем, как представить объекты, состоящие из треугольников, и как манипулировать ими.
Для этого мы используем куб; это не самый простой 3D-объект, который можно создать из треугольников, но он будет удобен для иллюстрации некоторых проблем. Рёбра куба имеют длину в две единицы и параллельны осям координат, а его центр находится в точке начала координат:
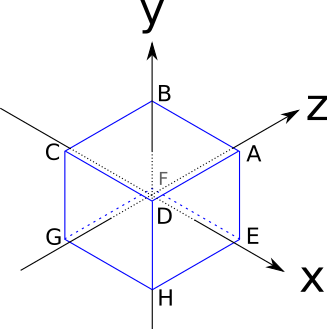
Вот координаты его вершин:
Стороны куба являются квадратами, однако мы знаем только как обращаться с треугольниками. Нет никаких проблем: любой полигон можно разложить на множество треугольников. Поэтому каждую сторону куба мы представим в виде двух треугольников.
Разумеется, не любое множество трёх вершин куба описывает треугольник на поверхности куба (например, AGH находится «внутри» куба), поэтому координат его вершин недостаточно для его описания; нам нужно также составить список треугольников, составленных из этих вершин:
A, B, C
A, C, D
E, A, D
E, D, H
F, E, H
F, H, G
B, F, G
B, G, C
E, F, B
E, B, A
C, G, H
C, H, DЭто показывает, что есть структура, которую можно использовать для представления любого составленного из треугольников объекта: список координат вершин и список треугольников, определяющий, какое множество из трёх вершин образует треугольники объекта.
Каждая запись в списке треугольников может содержать дополнительную информацию о треугольниках; например, мы можем хранить в нём цвет каждого треугольника.
Поскольку наиболее естественным способом хранения этой информации будут два списка, мы используем индексы списка в качестве ссылок на список вершин. То есть вышеприведённый куб можно представить следующим образом:
Vertexes
0 = ( 1, 1, 1)
1 = (-1, 1, 1)
2 = (-1, -1, 1)
3 = ( 1, -1, 1)
4 = ( 1, 1, -1)
5 = (-1, 1, -1)
6 = (-1, -1, -1)
7 = ( 1, -1, -1)
Triangles
0 = 0, 1, 2, red
1 = 0, 2, 3, red
2 = 4, 0, 3, green
3 = 4, 3, 7, green
4 = 5, 4, 7, blue
5 = 5, 7, 6, blue
6 = 1, 5, 6, yellow
7 = 1, 6, 2, yellow
8 = 4, 5, 1, purple
9 = 4, 1, 0, purple
10 = 2, 6, 7, cyan
11 = 2, 7, 3, cyanОтрендерить представленный таким образом объект довольно просто: сначала мы проецируем каждую вершину, сохраняем их во временном списке «спроецированных вершин»; затем мы проходим по списку треугольников, рендеря каждый отдельный треугольник. В первом приближении это будет выглядеть так:
RenderObject(vertexes, triangles) {
projected = []
for V in vertexes {
projected.append(ProjectVertex(V))
}
for T in triangles {
RenderTriangle(T, projected)
}
}
RenderTriangle(triangle, projected) {
DrawWireframeTriangle(projected[triangle.v[0]],
projected[triangle.v[1]],
projected[triangle.v[2]],
triangle.color)
}Мы не можем просто применить этот алгоритм к кубу, как есть, и надеяться на правильное отображение — некоторые из вершин находятся за камерой; а это, как мы уже видели, приводит к странному поведению. На самом деле, камера находится внутри куба.
Поэтому мы просто переместим куб. Чтобы сделать это, нам просто нужно сдвинуть каждую вершину куба в одном направлении. Давайте назовём этот вектор
Чтобы получить перемещённую версию
На этом этапе мы можем взять куб, переместить каждую вершину, а затем применить приведённый выше алгоритм, чтобы получить наконец наш первый 3D-куб:

Исходный код и рабочее демо >>
Модели и экземпляры
Но что если нам нужно отрендерить два куба?
Наивным подходом было бы создание ещё одного множества вершин и треугольников, описывающих второй куб. Это сработает, но займёт много памяти. А если мы захотим отрендерить миллион кубов?
Умнее будет думать в категориях моделей и экземпляров. Модель — это множество вершин и треугольников, описывающее объект как он есть (то есть "куб состоит из следующего множества вершин и треугольников"). С другой стороны, экземпляр модели — это конкретная реализация модели в некоторой позиции сцены (то есть "в (0, 0, 5) есть куб").
Преимущество второго подхода заключается в том, что каждый объект в сцене достаточно задать только один раз, после чего в сцену можно поместить произвольное количество экземпляров, просто описывая их позиции внутри сцены.
Вот грубое приближение того, как может быть описана подобная сцена:
model {
name = cube
vertexes {
...
}
triangles {
...
}
}
instance {
model = cube
position = (0, 0, 5)
}
instance {
model = cube
position = (1, 2, 3)
}Чтобы отрендерить её, нам нужно просто пройти по списку экземпляров; для каждого экземпляра создать копию вершин модели, применить к ним позицию экземпляра, а затем действовать как раньше:
RenderScene() {
for I in scene.instances {
RenderInstance(I);
}
}
RenderInstance(instance) {
projected = []
model = instance.model
for V in model.vertexes {
V' = V + instance.position
projected.append(ProjectVertex(V'))
}
for T in model.triangles {
RenderTriangle(T, projected)
}
}Заметьте, что для работы этого алгоритма координаты вершин модели должны быть определены в системе координат, «логичной» для объекта (это называется пространством модели). Например, куб определён таким образом, что его центр находится в (0, 0, 0); это значит, что когда мы говорим "куб расположен в (1, 2, 3)", мы имеем в виду "куб центрирован относительно (1, 2, 3)". При задании пространства модели нет никаких жёстких правил; в основном оно зависит от применения. Например, если у вас есть модель человека, то логично будет расположить точку начала координат у подошв его ног. Передвинутые вершины теперь будут выражаться в «абсолютной» системе координат сцены (называемой пространством мира).
Вот два куба:
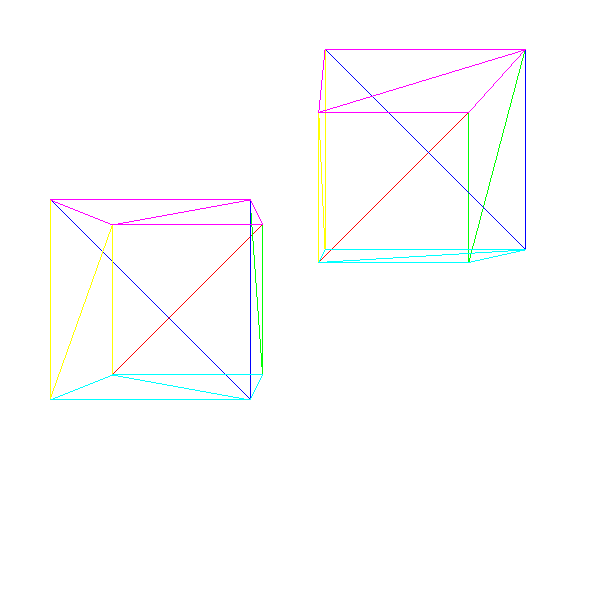
Исходный код и рабочее демо >>
Преобразование моделей
Данное выше определение сцены достаточно сильно нас ограничивает; в частности, поскольку мы можем указать только позицию куба, то способны создать сколько угодно экземпляров кубов, но все они будут ориентированы одинаково. В общем случае нам нужно иметь больше контроля над экземплярами; нам также хочется задавать их ориентацию, а возможно и масштаб.
Концептуально, мы можем задать преобразование модели точно с этими тремя элементами: коэффициентом масштаба, поворотом относительно точки начала координат пространства модели и перемещения в определённую точку сцены:
instance {
model = cube
transform {
scale = 1.5
rotation = <45 degrees around the Y axis>
translation = (1, 2, 3)
}
}Можно с лёгкостью расширить предыдущую версию псевдокода, добавив новые преобразования. Однако важен порядок применения этих преобразований; в частности, перемещение необходимо выполнять последним. Вот поворот на
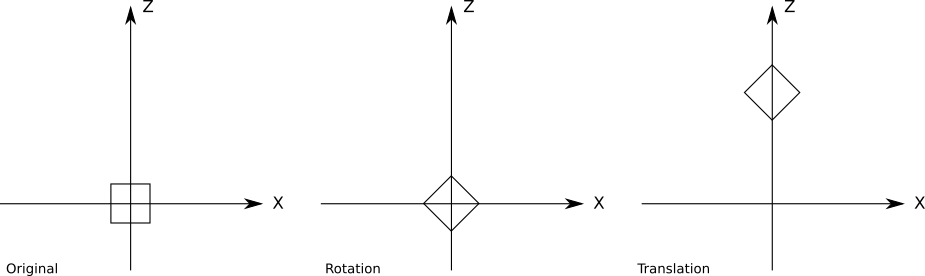
А вот перемещение, применённое до поворота:

Мы можем написать более общую версию
RenderInstance():RenderInstance(instance) {
projected = []
model = instance.model
for V in model.vertexes {
V' = ApplyTransform(V, instance.transform);
projected.append(ProjectVertex(V'))
}
for T in model.triangles {
RenderTriangle(T, projected)
}
}Метод
ApplyTransform() выглядит следующим образом:ApplyTransform(vertex, transform) {
V1 = vertex * transform.scale
V2 = V1 * transform.rotation
V3 = V2 + transform.translation
return V3
}Поворот выражается как матрица 3x3; если вы не знакомы с матрицами поворота, то пока считайте, что любой 3D-поворот можно представить как произведение точки на матрицу 3x3. См. подробнее в курсе линейной алгебры.
Преобразование камеры
В предыдущих разделах мы узнали, как можно расположить экземпляры моделей в разных точках сцены. В этом разделе мы узнаем, как двигать и поворачивать камеру в сцене.
Представьте, что вы висите посередине совершенно пустой системы координат. Всё окрашено в чёрный цвет. Внезапно прямо перед вами появляется красный куб. Мгновение спустя куб приближается на одну единицу к вам. Но приблизился ли куб к вам? Или вы сами передвинулись на одну единицу к кубу?
Поскольку у нас нет отправной точки, а систему координат не видно, мы никак не можем определить, что случилось.
Теперь куб повернулся вокруг вас на
Этот мысленный эксперимент показывает нам, что нет никакой разницы между перемещением камеры по фиксированной сцене и неподвижной камерой в движущейся и поворачивающейся вокруг неё сцене!
Преимущество такого очевидно эгоистичного видения вселенной заключается в том, что при фиксированной в точке начала координат камере, смотрящей в направлении
Будем считать, что у камеры тоже есть преобразование, состоящее из перемещения и поворота (масштаб мы опустим). Чтобы отрендерить сцену с точки обзора камеры, нам нужно применить к каждой вершине в сцене обратные преобразования:
V1 = V - camera.translation
V2 = V1 * inverse(camera.rotation)
V3 = perspective_projection(V2)Матрица преобразований
Давайте сделаем шаг назад и разберёмся, что происходит с вершиной
Сначала мы применяем преобразование модели, чтобы перейти из пространства модели в пространство мира:
V1 = V * instance.rotation
V2 = V1 * instance.scale
V3 = V2 + instance.translationЗатем мы применяем преобразование камеры, чтобы перейти из пространства мира в пространство камеры:
V4 = V3 - camera.translation
V5 = V4 * inverse(camera.rotation)Затем мы применяем уравнения перспективы:
vx = V5.x * d / V5.z
vy = V5.y * d / V5.zИ наконец мы привязываем координаты окна просмотра к координатам холста:
cx = vx * cw / vw
cy = vy * ch / vhКак вы видите, это довольно большой объём вычислений и для каждой вершины вычисляется множество промежуточных значений. Разве не будет удобно, если мы сократим всё это до единственного матричного произведения — возьмём
Давайте выразим преобразования в виде функций, получающих вершину и возвращающих преобразованную вершину. Пусть
В идеале нам бы хотелось иметь единственное преобразование, выполняющее то же, что и серия исходных преобразований, но имеющее гораздо более простое выражение:
Нахождение одной матрицы, представляющей
Однородные координаты
Рассмотрим выражение
Но давайте примем следующую договорённость: мы добавим к представлению четвёртый компонент, называемый
Такое представление имеет большой геометрический смысл. Например, при вычитании двух точек получается вектор:
При сложении двух векторов получается вектор:
Аналогично, можно легко увидеть, что при суммировании точки и вектора мы получаем точку, умножение вектора на скаляр даёт вектор, и так далее.
А что же представляют собой координаты с
Из всех этих представлений мы можем назвать представление с
То есть мы можем преобразовать декартовы координаты в однородные координаты, и обратно в декартовы координаты. Но как это поможет нам найти единое представление для всех преобразований?
Однородная матрица поворота
Давайте начнём с матрицы поворота. Выражение декартовой матрицы поворота 3x3 в однородных координатах тривиально; поскольку координата
Однородная матрица масштаба
Матрица масштабирования тоже тривиальна в однородных координатах, и она создаётся точно так же, как и матрица поворота:
Однородная матрица трансляции
Предыдущие примеры были простыми; они уже были представлены как умножения матриц в декартовых координатах, нам достаточно было добавить
Нам нужна такая матрица 4x4, что
Давайте сначала сосредоточимся на получении
Если мы раскроем векторное произведение, то получим
И из этого мы можем вывести, что
Применив те же рассуждения к остальным координатам, мы получим следующее матричное выражение для перемещения:
Однородная матрица проецирования
Сумму и произведение можно просто выразить как произведения матриц и векторов, которые являются суммами и произведениями. Но в уравнениях перспективного проецирования используется деление на
Есть большое искушение посчитать, что деление на
К счастью, в однородных координатах присутствует один случай деления: деление на координату
Заметьте, что эта матрица имеет размер
Здесь не хватает
Используя рассуждения, похожие на те, которые мы применяли для выведения матрицы трансляции, мы можем выразить перспективную проекцию как
Однородная матрица из окна просмотра на холст
Последний этап — размещение спроецированной на окно просмотра точки на холст. Это просто двухмерное преобразование масштаба с
На самом деле её легко скомбинировать с матрицей проецирования и получить простую матрицу преобразования из 3D в холст:
Практическое применение
Из практических соображений мы не будем использовать матрицу проецирования. Вместо этого мы используем преобразования модели и камеры, а затем преобразуем их результаты обратно в декартовы координаты следующим образом:
Это позволит нам выполнить ещё и другие операции в 3D до проецирования точек, которые нельзя выразить как матричные преобразования.
Снова матрица преобразования
Так как теперь мы можем выразить любое 3D-преобразование исходной вершины
И тогда преобразование вершины — просто вопрос вычисления следующего произведения:
Более того, мы можем разложить преобразование на две части:
Эти матрицы не нужно вычислять для каждой вершины (в этом и заключается смысл использования матрицы). На самом деле, их даже не обязательно вычислять в каждом кадре.
На очень высоком уровне псевдокод рендеринга сцены будет выглядеть так:
RenderModel(model, transform) {
projected = []
for V in model.vertexes {
projected.append(ProjectVertex(transform * V))
}
for T in model.triangles {
RenderTriangle(T, projected)
}
}
RenderScene() {
MCamera = MakeCameraMatrix(camera.position, camera.orientation)
for I in scene.instances {
M = MCamera*I.transform
RenderModel(I.model, M)
}
}Теперь мы можем отрисовать сцену, содержащую несколько экземпляров различных моделей, возможно, двигающихся и поворачивающихся, и можем двигать камеру по сцене.
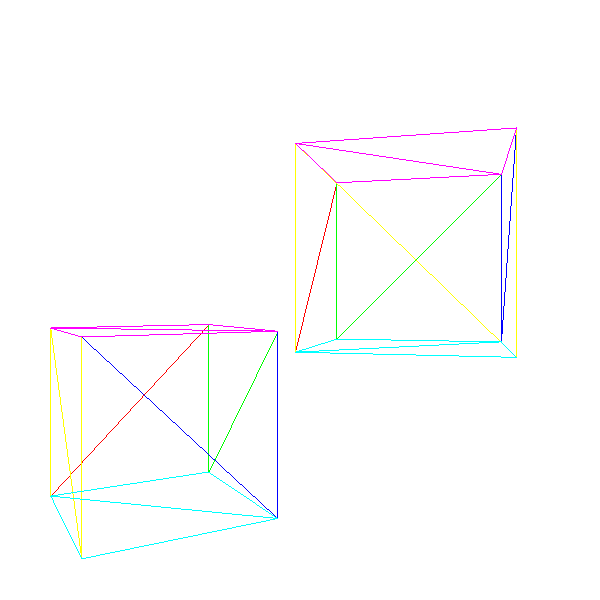
Исходный код и рабочее демо >>
Мы сделали большой шаг вперёд, но у нас по-прежнему есть два важных ограничения. Во-первых, при движении камеры объекты могут оказаться за ней, что создаёт всевозможные проблемы. Во-вторых, результат рендеринга выглядит не очень хорошо: он по-прежнему каркасный.
В следующей главе мы разберёмся с объектами, которые не должны быть видимы, а затем потратим оставшееся время на улучшение внешнего вида отрендеренных объектов.
Отсечение
В главе Перспективная проекция мы получили следующие уравнения:
Деление на
Чтобы избежать всех этих проблемных случаев, мы решили не рендерить ничего за плоскость проекции
Чем меньше операций мы делаем, тем быстрее будет наш рендерер, поэтому мы используем подход «сверху вниз». Рассмотрим сцену с несколькими объектами, каждый из которых состоит из четырёх треугольников.
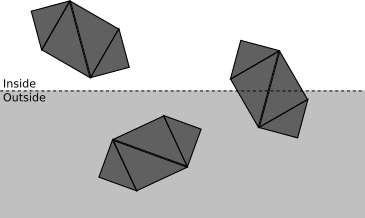
На каждом этапе мы стремимся как можно менее затратно определить, можно ли остановить отсечение на этой точке, или требуется дальнейшее и более подробное отсечение:
- Если объект полностью находится внутри объёма отсечения, то он принимается (выделен зелёным); если он полностью снаружи, то отбрасывается (красный):
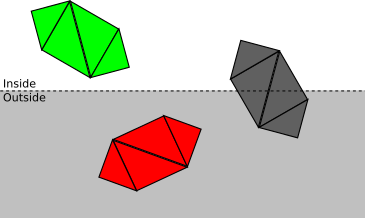
- В противном случае мы повторяем процесс для каждого треугольника. Если треугольник полностью находится внутри объёма отсечения, то он принимается, если полностью снаружи, то отбрасывается:
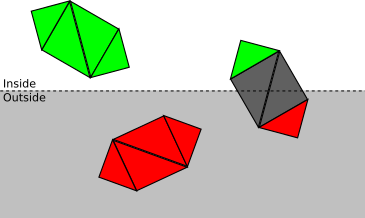
- В противном случае, нам нужно разбить сам треугольник. Исходный треугольник отбрасывается, и добавляются один или два треугольника, закрывающие часть треугольника, находящуюся внутри объёма отсечения:

Теперь мы подробноее рассмотрим каждый этап в процессе выполнения.
Задание плоскостей отсечения
Первое, что нужно сделать — найти уравнение плоскости отсечения. Нет ничего плохого в
Общее уравнение 3D-плоскости имеет вид
Заметьте, что если
Это очень удобная формулировка:
Как мы видели ранее, если
то есть
Объём отсечения
Хотя при использовании одной плоскости отсечения, позволяющей гарантировать, что объекты за камерой не будут рендериться, мы получаем правильные результаты, это не совсем эффективно. Некоторые объекты могут находиться перед камерой, но всё равно не быть видимыми; например, проекция объекта рядом с плоскостью проекции, но расположенная очень далеко вправо, выпадет из окна просмотра, и потому будет невидимой:
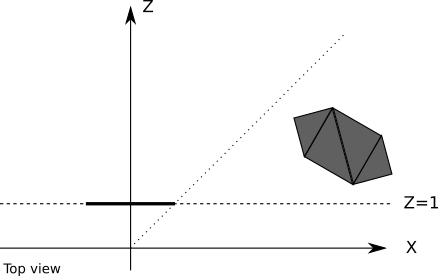
Все ресурсы, которые мы используем для вычисления проекции такого объекта, а также вычисления для треугольников и вершин, выполненные для его рендеринга, будут потрачены зря. Нам будет гораздо удобнее полностью игнорировать такие объекты.
К счастью, это совсем не сложно. Мы можем задать дополнительные плоскости, отсекающие сцену ровно до того, что будет видимо из окна просмотра; такие плоскости задаются камерой и обеими сторонами окна просмотра:
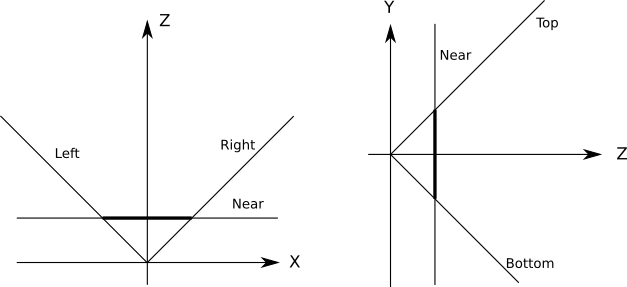
Все эти плоскости имеют
Для отсечения объектов или треугольников по объёму отсечения нам достаточно отсечь их по порядку каждой плоскостью. Все объекты, «выжившие» после отсечения одной плоскостью, отсекаются остальными плоскостями; это срабатывает, потому что объём отсечения является пересечением полупространств, задаваемых каждой плоскостью отсечения.
Отсечение целых объектов
Полностью задав объём отсечения его плоскостями отсечения, мы можем начать с определения того, находится ли объект полностью внутри или снаружи полупространства, задаваемого каждой из этих плоскостей.
Допустим, мы поместим каждую модель внутрь наименьшей сферы, которая может его содержать. Мы не будем рассматривать в статье, как это можно сделать; сферу можно вычислить из множества вершин одним из нескольких алгоритмов, или же приближение может быть задано разработчиком модели. В любом случае, будем считать, что у нас есть центр

Мы можем разбить пространственные отношения между сферой и плоскостью на следующие категории:
- Сфера целиком находится перед плоскостью. В этом случае модель принимается; дальнейшего отсечения относительно плоскости не требуется (однако она всё равно может отсекаться другой плоскостью):
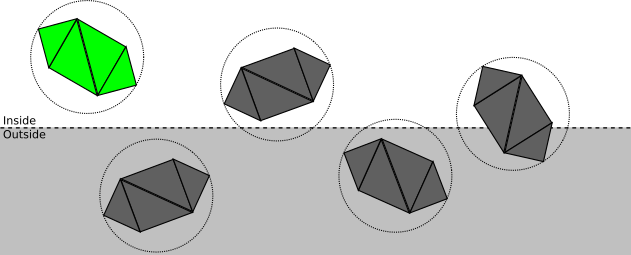
- Сфера целиком находится за плоскостью. В этом случае модель отбрасывается; дальнейшее отсечение не требуется (не важно, какими являются другие плоскости — ни одна часть модели не попадаёт внутрь объёма отсечения):
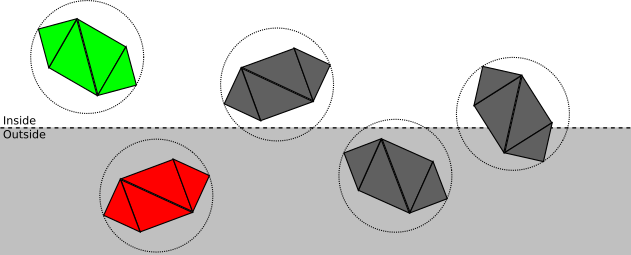
- Плоскость пересекается со сферой. Это не даёт нам достаточной информации о том, какие части объекта находятся внутри объёма отсечения; он может целиком находиться внутри, полностью снаружи, или частично внутри. Необходимо перейти к следующему этапу и отсечь модель треугольник за треугольником.
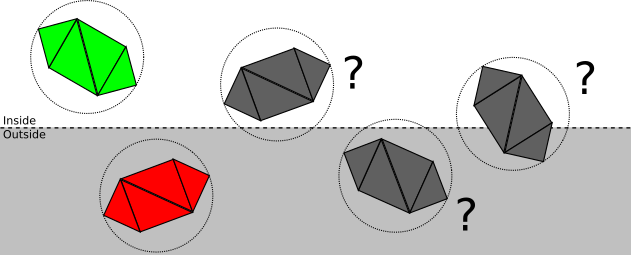
Как же на самом деле выполняется это разбиение на категории? Мы выбрали способ выражения плоскостей отсечения таким образом, что подстановка любой точки в уравнение плоскости даёт нам расстояние со знаком от точки до плоскости; в частности, мы можем вычислить расстояние со знаком
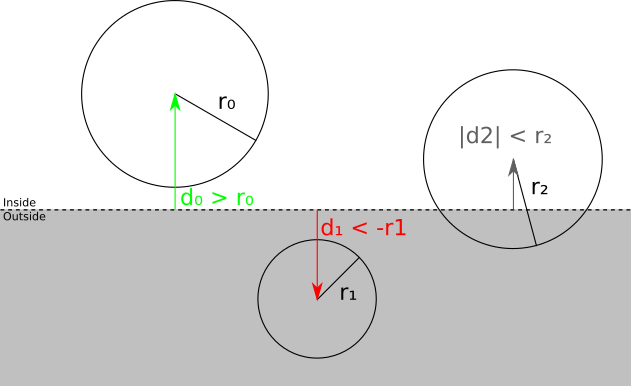
Отсечение треугольников
Если проверки сфера-плоскость недостаточно для определения того, находится ли объект полностью перед или полностью за плоскостью отсечения, то необходимо отсечь относительно неё каждый треугольник.
Мы можем классифицировать каждую вершину треугольника относительно плоскости отсечения, взяв знак расстояния со знаком до плоскости. Если расстояние равно нулю или положительно, то вершина находится перед плоскостью отсечения, в противном случае — за ней:
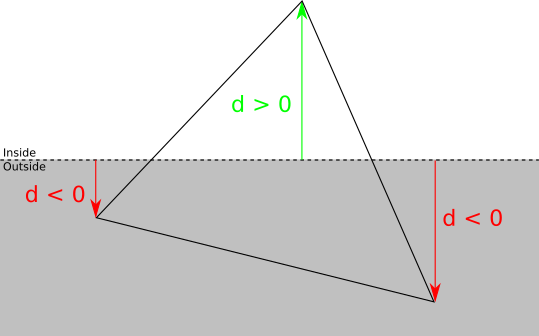
Существует четыре возможных случая:
- Три вершины находятся перед плоскостью. В таком случае весь треугольник находится перед плоскостью отсечения, поэтому он принимается без дальнейшего отсечения относительно этой плоскости.
- Три вершины находятся за плоскостью. В этом случае весь треугольник находится за плоскостью отсечения, поэтому он отбрасывается без дальнейших отсечений.
- Одна вершина находится перед плоскостью. Пусть
— вершина треугольника
, которая находится перед плоскостью. В этом случае
отбрасывается, и добавляется новый треугольник
, где
и
— пересечения
и
с плоскостью отсечения.
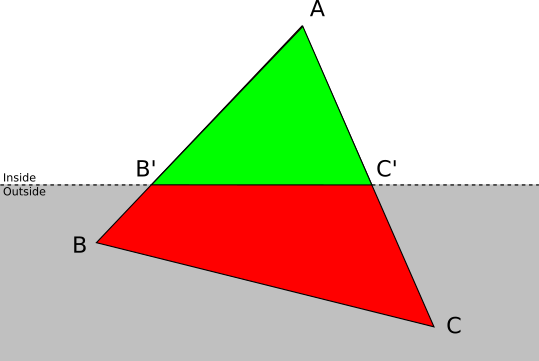
- Две вершины находятся перед плоскостью. Пусть
и
— вершины треугольника
, находящиеся перед плоскостью. В этом случае ABC отбрасывается, и добавляются два новых треугольника:
и
, где
и
— пересечения
и
с плоскостью отсечения.
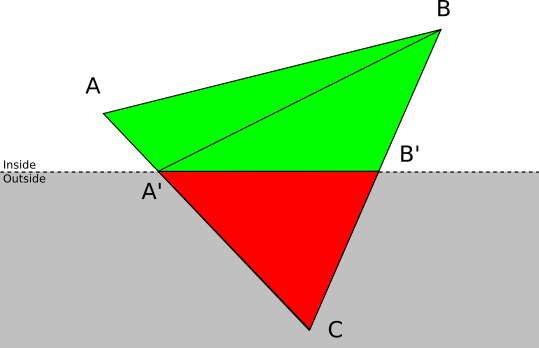
Пересечение отрезка и плоскости
Чтобы выполнить отсечение для каждого треугольника, нам нужно вычислить пересечение сторон треугольника с плоскостью отсечения. Надо заметить, что недостаточно вычислить координаты пересечения: необходимо также вычислить соответствующее значение атрибутов, связанных с вершинами, например, затенения, которое мы делали в главе Отрисовка затенённых треугольников, или одного из атрибутов, описанных в последующих главах.
У нас есть плоскость отсечения, заданная уравнением
Воспользовавшись линейными свойствами скалярного произведения, получаем:
Вычисляем
Мы знаем, что решение существует всегда, потому что
Вычислив
Заметьте, что
Отсечение в конвейере
Порядок глав статьи не соответствует порядку операций, выполняемых в конвейере рендеринга; как объяснено во введении, главы расположены в таком порядке, чтобы можно было как можно быстрее достичь наглядного прогресса.
Отсечение — это 3D-операция; она получает два 3D-объекта в сцене и генерирует новое множество 3D-объектов в сцене, а именно, пересечение сцены и объёма отсечения. Должно быть понятно, что отсечение должно выполняться после того, как объекты были размещены в сцене (то есть использованы вершины после преобразований модели и камеры), но перед перспективным проецированием.
Представленные в этой главе техники надёжно работают, но они очень общие. Чем больше мы будем заранее знать о сцене, тем эффективнее будет отсечение. Например, многие игры предварительно обрабатывают игровые карты, добавляя на них информацию о видимости; если получится разделить сцену на «комнаты», то можно создать таблицу с перечислением комнат, видимых из каждой конкретной комнаты. При рендеринге сцены в дальнейшем вам просто нужно выяснить, в какой комнате находится камера, после чего можно игнорировать все комнаты, помеченные как «невидимые» из неё, экономя значительные ресурсы при рендеринге. Конечно, при этом приходится тратить больше времени на предварительную обработку, а сцена получается более жёстко заданной.
Удаление скрытых поверхностей
Теперь, когда мы можем отрендерить любую сцену с любой точки обзора, давайте усовершенствуем нашу каркасную графику.
Очевидным первым шагом будет придание сплошным объектам сплошного внешнего вида. Для этого давайте используем
DrawFilledTriangle() для отрисовки каждого треугольника случайным цветом, и посмотрим, что из этого получится: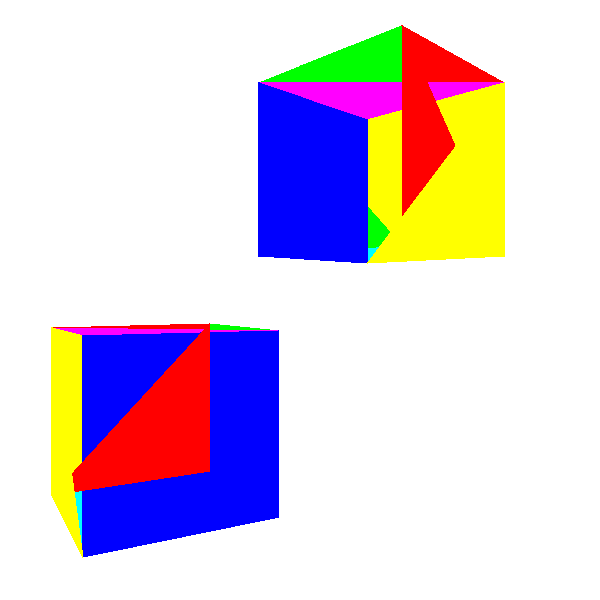
Не очень похоже на кубы, правда?
Проблема здесь в том, что некоторые треугольники, которые должны быть за другими, отрисовываются перед ними. Почему? Потому что мы просто отрисовываем 2D-треугольники на холсте практически в случайном порядке — в том порядке, который получился при задании модели.
Однако при задании треугольников модели нет «правильного» порядка. Предположим, что треугольники модели отсортированы таким образом, что сначала отрисовываются задние грани, а затем они перекрываются передними гранями. Мы получим ожидаемый результат. Однако если мы повернём куб на
Алгоритм художника
Первое решение этой проблемы известно как "алгоритм художника". Художники в реальном мире сначала отрисовывают фон, а затем закрывают его части передними объектами. Мы можем достичь того же эффекта, взяв каждый треугольник сцены, применив преобразования модели и камеры, отсортировав их сзади вперёд и отрисовав их в этом порядке.
Хотя при этом треугольники отрисуются в правильном порядке, этот алгоритм имеет недостатки, делающие его непрактичным.
Во-первых, он не очень хорошо масштабируется. Самый лучший алгоритм сортировки имеет скорость
Во-вторых, он требует одновременного знания всего списка треугольников. На это требуется много памяти, и не позволяет использовать потоковый подход к рендерингу. Если воспринимать рендеринг как конвейер, в котором треугольники модели входят с одного конца, а с другого выходят пиксели, то невозможно начать выводить пиксели, пока не будет обработан каждый треугольник. В свою очередь это означает, что мы не можем распараллелить этот алгоритм.
В-третьих, даже если вы смиритесь с этими ограничениями, то всё равно существуют случаи, когда правильного порядка треугольников не существует. Рассмотрим следующий случай:
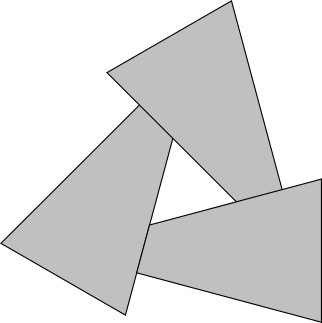
Неважно, в каком порядке вы будете отрисовывать эти треугольники — вы всегда будете получать неверный результат.
Буфер глубин
Если решение проблемы на уровне треугольников не срабатывает, то решение на уровне пикселей точно сработает, и в то же время оно преодолевает все ограничения алгоритма художника.
В сущности, каждый пиксель холста мы хотим закрасить «правильным» цветом. В этом случае, «правильный» цвет — это цвет ближайшего к камере объекта (в нашем случае
Оказывается, что мы можем запросто это сделать. Предположим, что мы храним значение
Представим такой порядок треугольников, при котором мы сначала хотим закрасить
Разумеется, мы получили верный результат вне зависимости от значений
С точки зрения реализации, нам нужен буфер для хранения координаты
Но откуда появляются значения
Они должны быть значениями
Итак, мы можем получить значения
И это ещё один способ применения алгоритма присвоения атрибутов. Почему бы не использовать
Z0, Z1 и Z2, вычисляем Z01, Z02 и Z02, получаем из них z_left и z_right, а затем вычисляем z_segment для каждого пикселя каждого горизонтального отрезка. И вместо выполнения вслепую PutPixel(x, y, color) мы делаем следующее:z = z_segment[x - xl]
if (z < depth_buffer[x][y]) {
canvas.PutPixel(x, y, color)
depth_buffer[x][y] = z
}Чтобы это сработало,
depth_buffer должен быть инициализирован значениями Получаемые результаты теперь гораздо лучше:

Исходный код и рабочее демо >>
Почему 1/Z вместо Z
Но на этом история не заканчивается. Значения
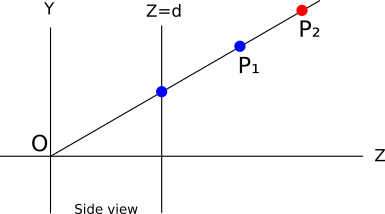
Чтобы проверить, насколько неверны значения, рассмотрим простой случай прямой из
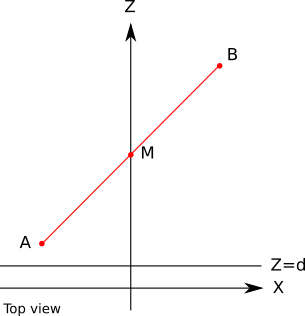
Давайте вычислим проекцию этих точек при
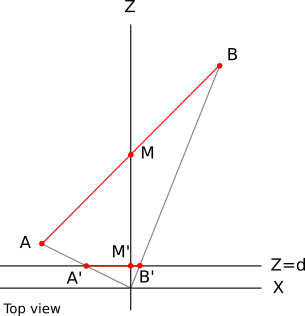
Что теперь произойдёт, если мы линейно проинтерполируем значения
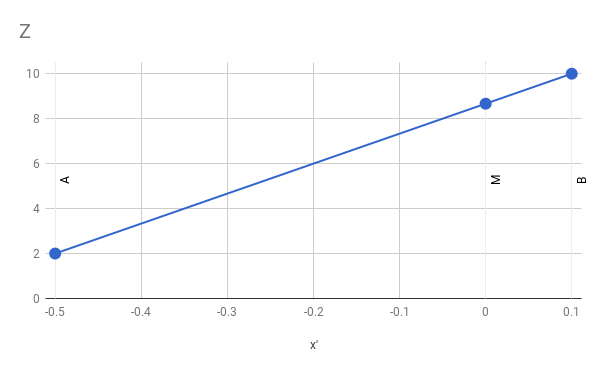
Из этого мы можем заключить, что
Если мы подставим числа и выполним арифметические вычисления, то получим
что очевидно не равно
Так в чём же проблема? Мы используем присвоение атрибутов, которое, как мы знаем, работает хорошо; мы передаём ему верные значения, которые получаются из данных; так почему же результаты неверны?
Проблема в том, что мы неявно подразумеваем, выполняя линейную интерполяцию: что интерполируемая нами функция линейна. А в нашем случае это не так!
Если
То есть для заданной разности экранных координат разность
Более формально, уравнение плоскости, содержащей изучаемый нами треугольник, имеет вид
С другой стороны, у нас есть уравнения перспективной проекции:
Мы можем снова получить из них
Если мы заменим
Умножив на
Что очевидно не является линейной функцией
Однако, если мы просто вычислим
Что очевидно является линейной функцией от
Чтобы показать, что это действительно работает, вот приведённый выше пример, но на этот раз вычисленный с помощью линейной интерполяции
И следовательно
Что на самом деле является правильным значением.
Всё это значит, что для буферизации глубин мы должны вместо значений
Отсечение задних граней
Буферизация глубин даёт нам нужные результаты. Но можем ли мы добиться того же более быстрым способом?
Вернёмся к кубу: даже если каждый пиксель в результате получает правильный цвет, некоторые из них перерисовываются снова и снова несколько раз. Например, если задняя грань куба рендерится до передней грани, то многие пиксели будут закрашиваться дважды. С увеличением количества операций, выполняемых для каждого пикселя (пока мы вычисляем для каждого пикселя только
Можем ли мы заранее отбросить пиксели, прежде чем выполнять все эти вычисления? Оказывается, мы можем отбрасывать целые треугольники ещё до того, как начнём отрисовку!
До этого момента мы говорили о передних гранях и задних гранях неформально. Представьте, что у каждого треугольника есть две стороны; одновременно мы можем видеть только одну из сторон треугольника. Чтобы разделить эти две стороны, мы добавим к каждому треугольнику стрелку, перпендикулярную его поверхности. Затем мы возьмём куб и убедимся, что каждая стрелка направлена наружу:
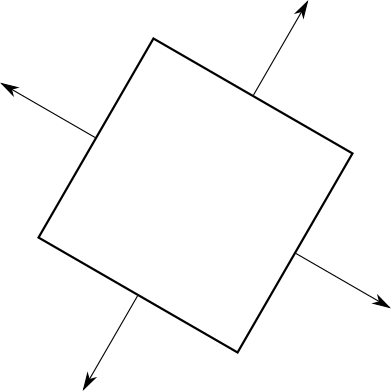
Теперь эта стрелка позволит нам классифицировать каждый треугольник как «передний» и «задний», в зависимости от того, направлен ли он к камере или от неё; если более формально, то если вектор просмотра и эта стрелка (на самом деле являющаяся вектором нормали треугольника) образуют угол соответственно меньше или больше
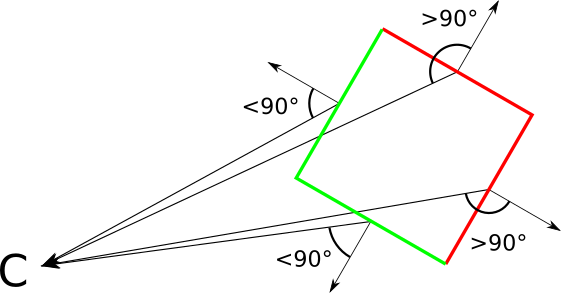
С другой стороны, наличие одинаково ориентированных двусторонних треугольников, позволяет нам задать то, что находится «внутри» и «снаружи» замкнутого объекта. По определению мы не должны видеть внутренние части замкнутого объекта. Это значит, что у любого замкнутого объекта вне зависимости от расположения камеры передние грани полностью перекрывают задние.
Что в свою очередь означает, что нам вообще не нужно отрисовывать задние грани, потому что они всё равно будут перерисовываться передними гранями!
Классификация треугольников
Давайте формализуем и реализуем это. Допустим, у нас есть вектор нормали треугольника
Мы снова можем воспользоваться свойствами скалярного произведения, чтобы ещё больше это упростить. Не забывайте, что если мы обозначим за
Поскольку
То есть классификация будет очень простой:
| Задняя грань | |
| Передняя грань |
Пограничный случай
Откуда мы берём вектор нормали? Оказывается, существует векторная операция — векторное произведение
Заметьте, что я сказал «направление вектора нормали», а не «вектор нормали». Для этого есть две причины. Первая заключается в том, что
Но вторая причина заключается в том, что если
Разумеется, в этом случае нам очень важно, в каком направлении указывает
Хотя векторное произведение не является коммутативным, оно и не случайно, конечно же.
Система координат, которую мы всё время использовали (X вправо, Y вверх, Z вперёд), называется левосторонней, потому что можно направить большой, указательный и средний палец левой руки в этих направлениях (большой палец вверх, указательный вперёд, средний вправо). Правосторонняя система координат похожа на неё, но указательный палец правой руки указывает влево.
Затенение
Давайте продолжим добавлять «реализма» сцене; в этой главе мы изучим, как добавить в сцену источники освещения и как осветить содержащиеся в ней объекты.
Эта глава называется Затенение, а не Освещение; это две тесно связанные, но отличающиеся концепции. Освещение относится к математике и алгоритмам, необходимым для вычисления воздействия освещения на одну точку сцены; Затенение использует техники для распространения воздействия источника освещения от дискретного множества точек на объекты целиком.
В главе Освещение раздела Трассировка лучей я уже рассказал всё необходимое, что нужно знать об освещении. Мы можем задать окружающее, точечное и направленное освещение; вычисление освещённости любой точки в сцене при заданной позиции и нормали поверхности в этой точке выполняется одинаковым способом и в трассировщике лучей, и в растеризаторе; теория точно такая же.
Более интересная часть, которую мы изучим в этой главе, заключается в том, как взять эту "освещённость в точке" и заставить её работать для объектов, состоящих из треугольников.
Плоское затенение
Давайте начнём с простого. Поскольку мы можем вычислить освещённость в точке, давайте просто выберем любую точку в треугольнике (скажем, его центр), вычислим там освещение и используем значение освещённости для затенения всего треугольника (для выполнения действительного затенения мы можем умножить цвет треугольника на значение освещённости):

Не так уж плохо. И очень просто увидеть, почему так случилось. Каждая точка в треугольнике имеет одну и ту же нормаль, и пока источник освещения достаточно далеко, векторы света приблизительно параллельны, то есть каждая точка получает примерно равное количество освещения. Это примерно объясняет различия между двумя треугольниками, из которых состоит каждая сторона куба.
Но что произойдёт, если мы возьмём объект, у которого каждая точка имеет свою нормаль?

Не очень хорошо. Совершенно очевидно, что объект является не настоящей сферой, а приближением, состоящим из плоских треугольных фрагментов. Поскольку такой тип освещения делает изогнутые объекты похожими на плоские, он называется плоским затенением.
Затенение по Гуро
Как же нам улучшить картинку? Простейший способ, для которого у нас уже имеются почти все инструменты — вычисление освещения не центра треугольника, а его трёх вершин; эти значения освещения от
Это называется затенением по Гуро по имени Анри Гуро, придумавшего эту идею в 1971 году. Вот результаты его применения к кубу и сфере:

Куб выглядит немного лучше; неравномерность теперь пропала, потому что оба треугольника каждой стороны имеют две общие вершины, и разумеется освещённость для них обеих вычисляется совершенно одинаково.
Однако сфера по-прежнему выглядит гранёной, а неоднородности на её поверхности выглядят очень неправильными. Это не должно нас удивлять, потому что в конце концов мы работаем со сферой как с набором плоских поверхностей. В частности, мы используем для соседних граней очень отличающиеся нормали — и в частности, мы вычисляем освещённость одной и той же вершины с помощью очень отличающихся нормалей разных треугольников!
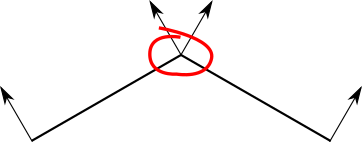
Давайте сделаем шаг назад. То, что мы используем плоские треугольники для представления изогнутого объекта, ограничивает наши техники, но не свойство самого объекта.
Каждая вершина в модели сферы соответствует точке в сфере, но задаваемые ими треугольники являются простым приближением поверхности сферы. Поэтому неплохо было бы, чтобы вершины представляли свои точки сферы как можно точнее — и это значит, среди прочего, что они должны использовать настоящие нормали сферы:
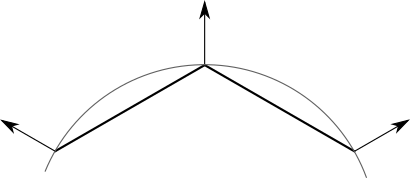
Однако это не относится к кубу; даже несмотря на то, что треугольники имеют общие позиции вершин, каждую грань нужно затенять независимо от остальных. У вершин куба нет единственной «верной» нормали.
Как же решить эту дилемму? Проще, чем кажется. Вместо вычисления нормалей треугольников, мы сделаем их частью модели; таким образом, разработчик объекта может использовать нормали для описания кривизны поверхности (или её отсутствия). Также, чтобы учесть случай куба и других поверхностей с плоскими гранями, мы сделаем нормали вершин свойством вершины в треугольнике, а не самой вершины:
model {
name = cube
vertexes {
0 = (-1, -1, -1)
1 = (-1, -1, 1)
2 = (-1, 1, 1)
...
}
triangles {
0 = {
vertexes = [0, 1, 2]
normals = [(-1, 0, 0), (-1, 0, 0), (-1, 0, 0)]
}
...
}
}Вот сцена, отрендеренная с помощью затенения Гуро при соответствующих нормалях вершин:

Куб по-прежнему выглядит как куб, а сфера теперь выглядит гораздо более похожей на сферу. На самом деле, взглянув на её контур, можно определить, что она составлена из треугольников (эту проблему можно решить использованием большего количества мелких треугольников, потратив больше вычислительной мощности).
Однако иллюзия разрушается, когда мы пытаемся рендерить блестящие объекты; зеркальный засвет на сфере потрясающе нереалистичный.
Есть здесь и более мелкая проблема: когда мы сдвигаем точечный источник очень близко к большой грани, мы естественно ожидаем, что она будет выглядеть ярче, а эффект зеркальности будет более явным; однако мы получаем строго противоположную картину:

Что здесь происходит: несмотря на то, что мы ожидаем, что точки рядом с центром треугольника получат больше освещения (потому что
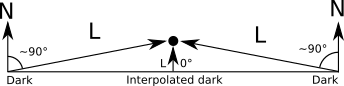
Затенение по Фонгу
Ограничения затенения по Гуро легко преодолеть, но как обычно существует компромисс между качеством и затрачиваемыми ресурсами.
При плоском затенении использовалось единственное вычисление освещения на треугольник. Для затенения по Гуро требовалось три вычисления освещения на треугольник плюс интерполяция единственного атрибута (освещённости) по треугольнику. Следующим шагом в этом увеличении качества и затрат на пиксель будет вычисление освещения для каждого пикселя треугольника.
Это не кажется особо сложным с точки зрения теории; в конце концов, мы уже вычисляли освещение для трёх точек, и вычисляли попиксельное освещение для трассировщика лучей. Но хитрость здесь в том, чтобы выяснить, откуда берутся входные данные для уравнения освещённости.
Нам нужен
У нас есть проекция
а также у нас есть интерполированное, но геометрически верное значение для
Поэтому мы можем получить из этих значений
Нам нужен
Нам нужен
Эта техника называется затенением по Фонгу по имени Буи Тьена Фонга, придумавшего её в 1973 году. Вот её результаты:

Исходный код и рабочее демо >>
Сфера выглядит отлично, за исключением её контура (но алгоритм затенения в этом не виновать), а эффект от приближения источника света к треугольнику ведёт себя именно так, как мы ожидаем.
Это также решает проблему с приближением источника к грани, теперь мы получаем ожидаемые результаты:

На этом этапе мы уже достигли возможностей трассировщика лучей, разработанного в первой части, за исключением теней и отражений. Вот выходные данные разрабатываемого нами растеризатора при использовании той же сцены:

А вот версия с трассировкой лучей для справки:

Они выглядят почти аналогично, несмотря на то, что в них используются совершенно различные технологии. Это логично, потому что мы использовали разные техники для рендеринга одной сцены. Единственным заметным различием являются рёбра сфер, которые трассировщик лучей рендерит как математически идеальные сферы, а растеризатор аппроксимирует как множество треугольников.
Текстуры
Пока мы можем рендерить такие объекты, как кубы или сферы, и воздействовать на них освещением. Но обычно нам нужно рендерить не кубы и сферы, а ящики и планеты, игровые кости или мрамор.
Рассмотрим деревянный ящик. Как превратить куб в деревянный ящик? Один из вариантов — добавить множество треугольников, поссоздающих структуру дерева, шляпки гвоздей, и так далее. Это сработает, но из-за геометрическая сложность сцены сильно повысится, что повлияет на производительность.
Ещё один вариант — имитировать ящик: взять плоскую поверхность куба и просто нарисовать поверх неё что-то, напоминающее древесину. Если не приглядываться к ящику, то вы никогда не заметите разницы.
Мы воспользуемся вторым подходом. Во-первых, нам понадобится изображение, которое мы будем рисовать на поверхности; в этом контексте мы назовём это изображение текстурой, хотя это и противоположно тому, что мы называем текстурой объекта — грубый он или мягкий, и т.д… Вот текстура «деревянного ящика»:

Текстура Filter Forge — Attribution 2.0 Generic (CC BY 2.0)
Во-вторых, нам нужно указать, как текстура должна накладываться на модель. Мы можем задать наложение для каждого треугоьника, указав точки текстуры, накладываемые на каждую вершину треугольника:

Стоит заметить, что без проблем можно деформировать текстуру или использовать только части текстуры, меняя координаты текстуры для каждой вершины.
Чтобы задать это наложение, мы используем систему координат, определяющую точки этой текстуры; назовём эти координаты
Основная идея наложения текстур проста: вычисляем координаты
Но у нас есть только координаты

…заурядные результаты. Ящики выглядят вполне неплохо, но если присмотреться к диагональным доскам, то становится очевидно, что они немного деформированы.
В чём же ошибка?
Мы снова попались в ловушку неверного предположения; мы считаем, что

Ситуация очень похожа на ту, которая встречалась нам в главе Буферизация глубин, и решение тоже очень похоже: хотя
При этом мы получим ожидаемые результаты:

Исходный код и рабочее демо >>