Comments 18
И вот же что обидно — чем ниже боковые лепестки, тем шире основной… Нет в мире совершенства. Прям квантовая неопределенность какая-то
+1
На сколько я понимаю, уменьшая уровень боковых лепестков вы уменьшаете количество энергии приходящиеся на эти частоты, но т.к. энергия сигнала постоянна (по закону сохранения энергии), то она перераспределяется на центральный лепесток и он становится шире.
+1
Сюда не нужно энергию привлекать — это же математика, а не физика. Подавление боковых лепестков происходит за счёт сложения в противофазе сдвинутых sinc-функций — и это же неизбежно расширяет основной лепесток.


0
В линейных системах да. Есть такой метод как spatially variant apodization, SVA. https://www.elibrary.ru/item.asp?id=35168232
0
Вы будете смеяться, но математическая природа этого эффекта точно такая же, что и у принципа неопределенности Гейзенберга. Принцип конфликта локализации по времени и частоте. Произведение ширины импульса во временной области на ширину в частотной области не может быть меньше некоторой константы.
0
Моё понимание неопределенности Гейзенберга довольно наивное и состоит в том, что для измерения характеристик физического объектов на него надо воздействовать, а любое воздействие изменяет эти самые характеристики. В математике процесс исследования свойства объекта не меняет, а похожие свойства являются лишь особенностями отдельно взятого инструмента. В частности, зависимость локализации от частоты при спектральном анализе через преобразование Фурье легко разрешается в непрерывном вейвлет-преобразовании, где такой зависимости нет.
0
для измерения характеристик физического объектов на него надо воздействовать
Дело не только в этом. Измерительное воздействие, даже на микроуровне, можно контролировать. Однако квантовые величины, которые не подлежат одновременной локализации, связаны друг с другом через преобразование Фурье. И именно из-за невозможности одновременной локализации по времени и частоте и происходит невозможность одновременного точного измерения этих величин, или хотя бы принудительного сообщения частице точной их комбинации. В Википедии об этом прямо сказано:
"Соотношение неопределённостей в квантовой механике в математическом смысле есть прямое следствие некоего свойства преобразования Фурье[* 5]."
легко разрешается в непрерывном вейвлет-преобразовании, где такой зависимости нет
В непрерывном вейвлет-преобразовании такая зависимость есть. Вы можете выбирать ширину базового вейвлета (количество периодов колебаний в нём) во времени. Когда в вейвлете мало колебаний — то он хорошо локализован во времени и плохо локализован по частоте, и наоборот. В зависимости от ширины вейвлета результаты времячастотного анализа могут сильно различаться для одного и того же сигнала.
0
Я может чего-то не понимаю. Вот например — 1 кГц составляющая из некоторого сигнала:
Достаточно хорошо локализован по частоте, что можно увидеть через FFT:
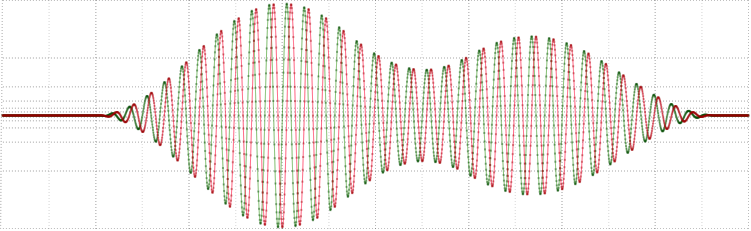
Теперь приводим её к аналитическому виду через преобразование Гильберта (красным цветом — мнимая составляющая)
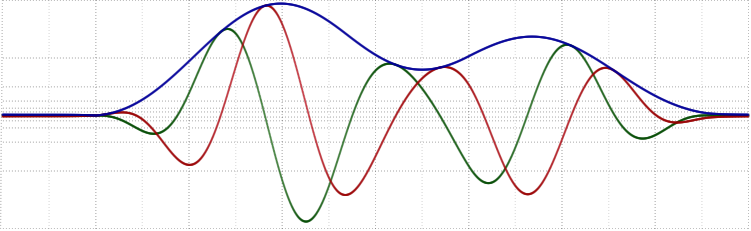
И получаем её огибающую через абсолютное значение
На этой огибающей есть локальные максимумы, которые тоже достаточно хорошо локализованы во времени. Для 100 Гц получим ту же картину
рис.
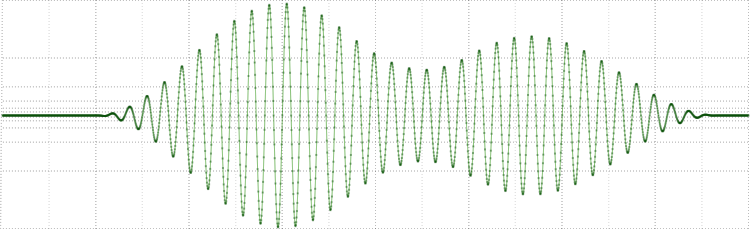

Достаточно хорошо локализован по частоте, что можно увидеть через FFT:
рис.


Теперь приводим её к аналитическому виду через преобразование Гильберта (красным цветом — мнимая составляющая)
рис.

И получаем её огибающую через абсолютное значение
рис.


На этой огибающей есть локальные максимумы, которые тоже достаточно хорошо локализованы во времени. Для 100 Гц получим ту же картину
рис.

0
«Достаточно хорошо локализован» — это значит «сжат в одну точку».
Предлагаю вам сгенерировать сигнал вида «frequency sweep» — синус с непрерывно меняющейся частотой. Например, так:
y = sin(2*pi*(100+50*t)*t),
где t — время. При изменении t между 0 и 1 частота будет меняться между 100 и 200Гц (могу объяснить, почему не 150Гц — но проверьте сначала сами!)
И пропустите этот сигнал через времячастотный анализ, основанный на непрерывном вейвлет-преобразовании. Вы увидите, что, хотя характер спектра в общем наблюдается, но линия имеет конечную ширину. В то время, как истинный спектр является бесконечно узкой линией. Варьируя ширину базового вейвлета, вы сможете менять ширину линии во времени и частоте, но никогда не добьётесь ее ужатия в бесконечно тонкую.
Также попробуйте следующий сигнал
y1 = sin(2*pi*f*t), где t — время, f — некоторая частота
y2 = delta(t — t0), где delta(x)={0 при x!=0, 1 при x=0}; t0 — некоторый момент времени
y = y1 + y2
И проанализируйте сигнал y. Вы увидите, что есть горизонтальная линия (от синуса) и вертикальная линия (от импульса), но обе линии будут несколько размазаны. А истинный спектр такого сигнала состоит из двух бесконечно тонких перпендикулярных прямых. Варьируя параметры анализа, вы сможете добиться сужения либо горизонтальной, либо вертикальной прямых, но не обеих вместе.
Произведение ширины горизонтальной и вертикальной прямых не сможет быть меньше некоторой константы, что и является прямой аналогией с принципом неопределенности Гейзенберга. Эта константа достигает минимального значения в случае использование вейвлетов Морлета (синус, модулированный гаусс-функцией).
Под «шириной линии» в данном случае понимается заключение в некоторый интервал заданной части интеграла от её квадрата. Ведь гаусс-функция не равна строго нулю на всей числовой оси. Иные критерии «ширины линии» приводят к другим оптимальным вейвлет-базисам.
Предлагаю вам сгенерировать сигнал вида «frequency sweep» — синус с непрерывно меняющейся частотой. Например, так:
y = sin(2*pi*(100+50*t)*t),
где t — время. При изменении t между 0 и 1 частота будет меняться между 100 и 200Гц (могу объяснить, почему не 150Гц — но проверьте сначала сами!)
И пропустите этот сигнал через времячастотный анализ, основанный на непрерывном вейвлет-преобразовании. Вы увидите, что, хотя характер спектра в общем наблюдается, но линия имеет конечную ширину. В то время, как истинный спектр является бесконечно узкой линией. Варьируя ширину базового вейвлета, вы сможете менять ширину линии во времени и частоте, но никогда не добьётесь ее ужатия в бесконечно тонкую.
Также попробуйте следующий сигнал
y1 = sin(2*pi*f*t), где t — время, f — некоторая частота
y2 = delta(t — t0), где delta(x)={0 при x!=0, 1 при x=0}; t0 — некоторый момент времени
y = y1 + y2
И проанализируйте сигнал y. Вы увидите, что есть горизонтальная линия (от синуса) и вертикальная линия (от импульса), но обе линии будут несколько размазаны. А истинный спектр такого сигнала состоит из двух бесконечно тонких перпендикулярных прямых. Варьируя параметры анализа, вы сможете добиться сужения либо горизонтальной, либо вертикальной прямых, но не обеих вместе.
Произведение ширины горизонтальной и вертикальной прямых не сможет быть меньше некоторой константы, что и является прямой аналогией с принципом неопределенности Гейзенберга. Эта константа достигает минимального значения в случае использование вейвлетов Морлета (синус, модулированный гаусс-функцией).
Под «шириной линии» в данном случае понимается заключение в некоторый интервал заданной части интеграла от её квадрата. Ведь гаусс-функция не равна строго нулю на всей числовой оси. Иные критерии «ширины линии» приводят к другим оптимальным вейвлет-базисам.
0
«Достаточно хорошо локализован» — это значит «сжат в одну точку».Думаю, что локальный максимум вполне подходит под «одну точку» — потому что однозначно определяется через равенство нулю производной. Также думаю, что эти максимумы можно привести к импульсному виду методами обратной свёртки — другой вопрос, что сделать это непросто.
Предлагаю вам сгенерировать сигнал вида «frequency sweep» — синус с непрерывно меняющейся частотойЭто называется ЛЧМ — линейная частотная модуляция. И оперирует она не частотой, а мгновенной частотой, что совсем не одно и то же. В ответ могу предложить сгенерировать ЛЧМ длительностью в один семпл и посмотреть, как меняется сигнал в зависимости от граничных частот (спойлер: никак). Если вы хотите получить бесконечно тонкую линию, то и использовать нужно соответствующий метод — а именно частотную демодуляцию, которая в единицу времени возвращает одну конкретную (мгновенную) частоту, а не сумму частот как у Фурье-преобразования, и не модулированную по амплитуде частоту как у непрерывного вейвлет-преобразования.
P.S. На всякий случай хочу напомнить, что мой изначальный комментарий был о том, что привлечение к рассматриваемому вопросу понятий из физики никак не поможет в задаче уменьшения уровня боковых лепестков, поскольку мат.аппарат для этого используется совсем другой.
0
Думаю, что локальный максимум вполне подходит под «одну точку» — потому что однозначно определяется через равенство нулю производной
В принципе неопределенности Гейзенберга речь идет о принципиальной невозможности неограниченной локализации, поэтому говорить, что «а не очень-то и хотелось» — некорректно. Локализация или возможна, или невозможна.
Локальный минимум или максимум можно взять как точное местоположение сигнала во времени или частоте. Однако вы не сможете таким образом отличить друг от друга сигналы, которые действительно локализованы в одной или другой области (как единичный импульс или чистая синусоида) от «размазанных» сигналов, имеющих сплошной спектр с конечной шириной линий. Ведь можно сгенерировать сигнал, спектр которого будет не линией, а гаусс-функцией.
соответствующий метод — а именно частотную демодуляцию, которая в единицу времени возвращает одну конкретную (мгновенную) частоту
Речь шла о непрерывном вейвлет-преобразовании, а не других методах. Я всего лишь привел контр-пример к вашему утверждению: «зависимость локализации от частоты при спектральном анализе через преобразование Фурье легко разрешается в непрерывном вейвлет-преобразовании, где такой зависимости нет».
Более того, независимо от того, какой используется метод анализа — просто не существует таких сигналов, которые бы были одновременно локализованы и по времени, и по частоте, так, чтобы произведение их ширины в одной и другой области было меньше некоторой константы.
мой изначальный комментарий был о том, что привлечение к рассматриваемому вопросу понятий из физики никак не поможет в задаче уменьшения уровня боковых лепестков
Я изначально отвечал не на ваш комментарий, а на вот этот. Человек предположил, что в наблюдаемых закономерностях есть что-то сродни квантовой неопределенности, и я лишь хотел подвердить его предположение, больше ничего.
Хотя, конечно, это оффтопик. Прошу прощения.
0
Не за что извиняться и обсуждение вовсе не оффтопик, поскольку затрагивает важные сопутствующие темы. В предыдущем сообщении я спешил и не развернул достаточно свою мысль, сейчас попробую ещё раз.
y = sin(2*pi*(100+50*t)*t) + i*cos(2*pi*(100+50*t)*t)
где i — мнимая единица. Необходимость этого проистекает из того, что нельзя однозначно решить одно уравнение с двумя неизвестными — нужна система из двух уравнений. В данном случае неизвестными являются не только мгновенная частота, но и амплитуда, которая в данном случае имеет вид прямоугольного окна.
Но как и в случае обычных полиномиальных уравнений, когда при недостатке данных можно использовать методы типа наименьших квадратов, так и здесь можно пойти на хитрость — задав амплитуду константой и ограничив спектр (чего в вашем примере сделано не было), можно обойтись лишь одной составляющей, получая вторую на уровне приёмника аналитически.
Частота по определению обратно пропорционально периоду — поэтому вполне логично, что уменьшение ширины сигнала в одной области (ограниченного нулями) приводит к увеличению ширины сигнала в другой области и наоборот. Но из этого никаких неопределённостей не возникает — обратная пропорциональность ничем не хуже прямой пропорциональности. Частота вполне определённо существует на промежутке от минус бесконечности до плюс бесконечности с одной и той же амплитудой и фазой, а затухание сигнала или спектра в ноль возникает из-за суммирования разных частот.
Неопределённость возникает, когда бесконечность искуственно ограничивается определённым периодом. Но эта неопределённость является следствием того факта, что подобное ограничение искажает спектр сигнала, а вовсе не фундаментальной неопределённостью преобразования Фурье как такого. В частности, спектр гауссианы — это тоже гауссиана, и математически они бесконечны что во временной, что в частотной области.
Другой вид неопределённости — это когда сигнал является суммой нескольких. Очевидно, что если сумма двух синусоид с одной частотой дала ноль, то восстановить из этого нуля исходные 4 параметра никак не получится. Но и здесь можно пускаться на всякие хитрости, если заранее знать дополнительные факторы типа уровня шума, частоту модуляции, импульсную характеристику системы и всё такое.
«frequency sweep»Для того, чтобы однозначно восстановить исходную мгновенную частоту из этого сигнала, нужно генерировать не только синус, но и косинус — то есть брать сигнал
y = sin(2*pi*(100+50*t)*t) + i*cos(2*pi*(100+50*t)*t)
где i — мнимая единица. Необходимость этого проистекает из того, что нельзя однозначно решить одно уравнение с двумя неизвестными — нужна система из двух уравнений. В данном случае неизвестными являются не только мгновенная частота, но и амплитуда, которая в данном случае имеет вид прямоугольного окна.
Но как и в случае обычных полиномиальных уравнений, когда при недостатке данных можно использовать методы типа наименьших квадратов, так и здесь можно пойти на хитрость — задав амплитуду константой и ограничив спектр (чего в вашем примере сделано не было), можно обойтись лишь одной составляющей, получая вторую на уровне приёмника аналитически.
не существует таких сигналов, которые бы были одновременно локализованы и по времени, и по частоте, так, чтобы произведение их ширины в одной и другой области было меньше некоторой константы.
Частота по определению обратно пропорционально периоду — поэтому вполне логично, что уменьшение ширины сигнала в одной области (ограниченного нулями) приводит к увеличению ширины сигнала в другой области и наоборот. Но из этого никаких неопределённостей не возникает — обратная пропорциональность ничем не хуже прямой пропорциональности. Частота вполне определённо существует на промежутке от минус бесконечности до плюс бесконечности с одной и той же амплитудой и фазой, а затухание сигнала или спектра в ноль возникает из-за суммирования разных частот.
Неопределённость возникает, когда бесконечность искуственно ограничивается определённым периодом. Но эта неопределённость является следствием того факта, что подобное ограничение искажает спектр сигнала, а вовсе не фундаментальной неопределённостью преобразования Фурье как такого. В частности, спектр гауссианы — это тоже гауссиана, и математически они бесконечны что во временной, что в частотной области.
Другой вид неопределённости — это когда сигнал является суммой нескольких. Очевидно, что если сумма двух синусоид с одной частотой дала ноль, то восстановить из этого нуля исходные 4 параметра никак не получится. Но и здесь можно пускаться на всякие хитрости, если заранее знать дополнительные факторы типа уровня шума, частоту модуляции, импульсную характеристику системы и всё такое.
0
Автор, вот вам ссылка на статью про современные методы синтеза оконных функций, которые предоставляют просто-таки виртуозные возможности и взрывают моск:
R. Desbiens, P. Tremblay «A new efficient approach to the design of parametric windows with arbitrary sidelobe profiles», DOI:10.1016/j.sigpro.2006.01.011
R. Desbiens, P. Tremblay «A new efficient approach to the design of parametric windows with arbitrary sidelobe profiles», DOI:10.1016/j.sigpro.2006.01.011
+1
Спасибо за ссылку, интересная статья. Но в построении суммирующихся в единицу окон с заданным уровнем перекрытия (те самые заявленные во введении новые свойства) рассмотренные в ней методы не помогут.
0
R. Desbiens, P. Tremblay «A new efficient approach to the design of parametric windows with arbitrary sidelobe profiles»Внимательно изучил эту статью и должен сказать, что её авторы слегка недожали. В частности, не получится взять формулы из статьи, заполнить массив, сделать обратное FFT и получить вожделенное окно с n-равновысотными боковыми лепестками — а всё потому, что все рассуждения и вычисления они делают для непрерывного бесконечного спектра. Неладное можно заподозрить уже на том этапе, что в статье нет ни одного изображения окна во временном домене. Для периодического спектра все эти вычисления не подходят — потому что в нём спектром прямоугольного окна является не sin(x)/x, а sin(n·x)/sin(x) (периодический sinc). Соответственно и равновысотные лепестки нужно считать подбором коэффициентов у суммы именно периодических sinc, а не обычных.
0
Отдельно можно заметить, что авторы решают не реальную инженерную задачу, а сферического коня в вакууме (что для математиков весьма характерно). Всё потому что требование равновысотности n-первых боковых лепестков ничем не обоснована, а просто взята с потолка (ну или откуда там математики берут свои идеи). Убедиться в этом просто — достаточно взять и посмотреть на практике, что получится.
Поскольку готового решения в статье не обнаружилось (что тоже для математиков весьма характерно), возьмём окно Дольфа-Чебышева, у которого вообще все боковые лепестки равновысотные:
Поскольку готового решения в статье не обнаружилось (что тоже для математиков весьма характерно), возьмём окно Дольфа-Чебышева, у которого вообще все боковые лепестки равновысотные:
2048 точек, -50 дБ

И помножим его на синусоиду:
500 Гц (с дискретизацией в 48 кГц)

И вот таким получился спектр:
спектр

Как видно, вблизи основного лепестка ничего похожего на полку не наблюдается, равно как и симметрии лепестков относительно центра. Амплитуды лепестков выравниваются лишь на достаточном отдалении от центра, что в данном случае не имеет никакой ценности, а также превышают значение, заложенное в параметры окна (примерно на 5 дБ). Из этого всего следует, что для улучшения результата анализа тут требуются некоторые другие характеристики близлежащих к центру лепестков.
+1
Sign up to leave a comment.
Оконные функции своими руками