Comments 60
у меня один вопрос: машину времени создать можно или нет?
Говорят что можно, но она не работает
Вообще без проблем. Я себе даже сделал. Средняя "скорость" где-то 24 часа в сутки :)
Давно уже создана дембелями
В пространстве P1 за время t1 энтропия E возрастает на E1. Допустим, есть некая мера k, которая является множителем обращения энтропии. Чтобы обернуть энтропию, необходимо применить антиэнтропию в размере -kE1. А это значит, что где-то в другом пространстве P2 энтропия E должна увеличиться на kE1, чтобы антиэнтропию оттуда извлечь.
Если проще, чтобы стало холодно, надо где-то нагреть и потратить на это антиэнтропию, и там возрастёт энтропия.
Множитель k равен c^4 для нашего пространства. Машину времени уже изобрели, в прошлое можно переместиться, если конечно у тебя где-то есть параллельная вселенная, которую ты можешь уничтожить, пустив на антиэнтропию, а также есть достаточно времени и ресурсов, чтобы доработать машину времени из тех ресурсов, что есть.
По сути твоя машина времени будет считать наоборот, каждый квант во вселенной, и изменять его соответствующим образом. Это как в некоторых играх, чтобы вернуть игру на тридцать секунд назад, состояние игры вычисляется по кадрам задом на перёд с учётом всех команд сделанных игроком, но задом наперёд. Там нажимаешь кнопку назад и игра прокручивается назад.
Можно конечно локально откатить время назад, прямо как холодильник локально понижает температуру, и это сделали в размере одного кванта.
Осталось сделать это для всей вселенной, дерзай XD.
Теоретически машина времени возможна, у нас в НИИ даже собрали опытный образец. Но каждый раз за пять минут до пробного запуска, не пойми откуда, приходит какой-нибудь новичок лаборант и срывает экспиремент
Как-будто Vsauce посмотрел, браво
Какой кайф!
Картинки очень красивые, анимированные. Лайк за оформление. Но у меня вопрос: какое практическое применение этому знанию может быть? Это где-то в расчетах чего-то практичного используется? Механическая прочность? Аэродинамика? Динамика газов или жидкостей? Что угодно ещё? Или это просто игры разума, оторванные от реальности?
Преимущественно, теория хаоса ищет ответы на фундаментальные вопросы. Однако еë близкая родственница — теория катастроф уже помогает избегать неприятностей, типа бифуркаций Хопфа, приводящих к автоколебаниям: флаттеру крыла самолëта, раскачиванию балок или мостовых конструкций под действием ветровых нагрузок. Другие бифуркации, локальные или глобальные, помогают правильно понять динамику вулканических извержений, популяционных вспышек, и некоторых климатических явлений. На конференциях по теории хаоса я встречал доклады на темы касающиеся природы эпилепсии, фибрилляции сердечных мышц, проблем автоматизации дорожного движения, химических автокаталитических систем, спонтанной намагниченности метаматериалов и смены полюсов Земли. Первые работы по теории хаоса касались чисто практических проблем прогноза погоды и биржевых котировок. А уж модную в последние лет 20 самооорганизующуюся критичность, как источник "черных лебедей", вспоминают при любом удобном случае, где надо и где не надо, сейсмологи, социологи, эпидемиеологи и нейрофизиологи.
Мне самому доводилось принимать участие в чисто практической инженерной работе по избеганию хаотического режима в системе активного подавления колебаний подвески сиденья для водителя в карьерной технике.
Там где есть место математическому моделированию динамики нелинейных систем, надо быть готовым к тому, что модель или система может оказаться способной генерировать хаос и результаты моделирования будут лишь качественно соответствовать явлению.
Но у меня вопрос: какое практическое применение этому знанию может быть? Это где-то в расчетах чего-то практичного используется?
Практическое применение таково, что картинки дают понимание внутреннего устройства хаотических систем, а также того, как можно при помощи изменения параметров управлять ими, чтобы добиться желаемого поведения, например, превратить хаотическое движение в периодическое (а иногда, допустим, в криптографии, наоборот, добиться именно хаотического поведения). Хаотические процессы встречаются где угодно, и в аэродинамике, и в динамике газов и жидкостей
Картинки очень красивые, анимированные.Я бы даже так сформулировал основное правило для какого-нибудь робота, наблюдащего за визуальным представлением динамического процесса: «Как только картинка из скучной превращается в красивую — немедленно зови
Плохо только, что такие изменения часто происходят скачкообразно, и смертельно опасная красота приходит неожиданно
Но у меня вопрос: какое практическое применение этому знанию может быть?… Или это просто игры разума, оторванные от реальности?
Нелинейная динамика и мультистабильные состояния все шире и успешно используются для описания нейродинамики мозга и отдельных нейросетей, собственно носителей самого этого разума) См. эти обзоры 1, 2.
Практическое применение этому знанию может быть: процедурная генерация звука/графики/игровых миров/etc.
Картинки очень красивые, анимированные. Лайк за оформление. Но у меня вопрос: какое практическое применение этому знанию может быть?Мне иногда в голову приходит, что дискретные динамические системы (описываемые последовательностью состояний) в теории динамических систем играют примерно такую же роль, как дрозофилы в генетике, т.е. позволяют исследовать общие закономерности. А исследование систем, описываемых дифференциальными уравнениями — это уже аналог прикладной генетики, вроде выведения новых пород свиней или генно-модифицированных растений
Ирония состоит в том, что методы анализа дискретных систем опираются на топологию и анализ непрерывных отображений.
Даже если это так (не могу опровергнуть, в такие подробности я не погружался), дискретные отображения все равно проще устроены, их проще исследовать численными методами, а хаос для них может наблюдаться и в одномерном случае (для автономных систем ОДУ для возникновения хаоса нужна размерность не менее, чем 3)
Модели нелинейной динамики и её методы много где используются: При обработке медицинских данных, временных рядов, устойчивости движения. Вот вам пример из моего дисера. Для анализа файловой траектории ротора в турбонасосном агрегате жрд я использовал теорему Тэккинса для восстановления аттрактора, имея данные только с одного датчика
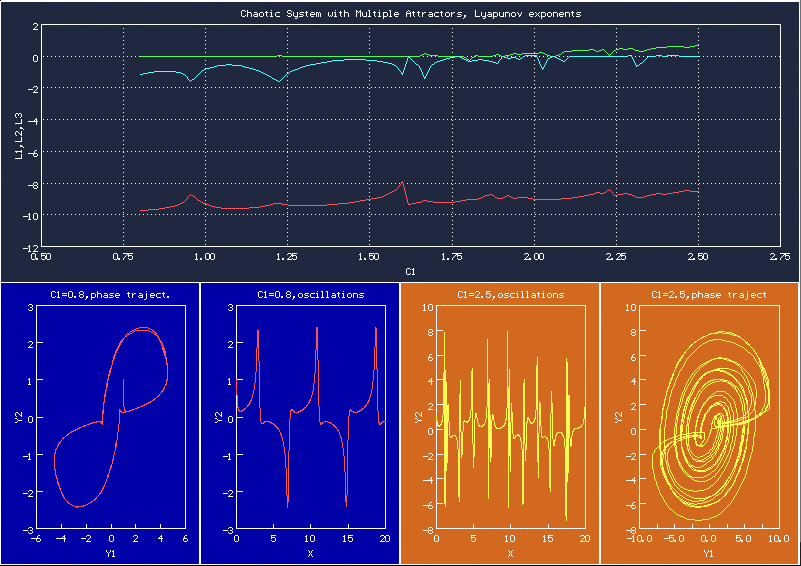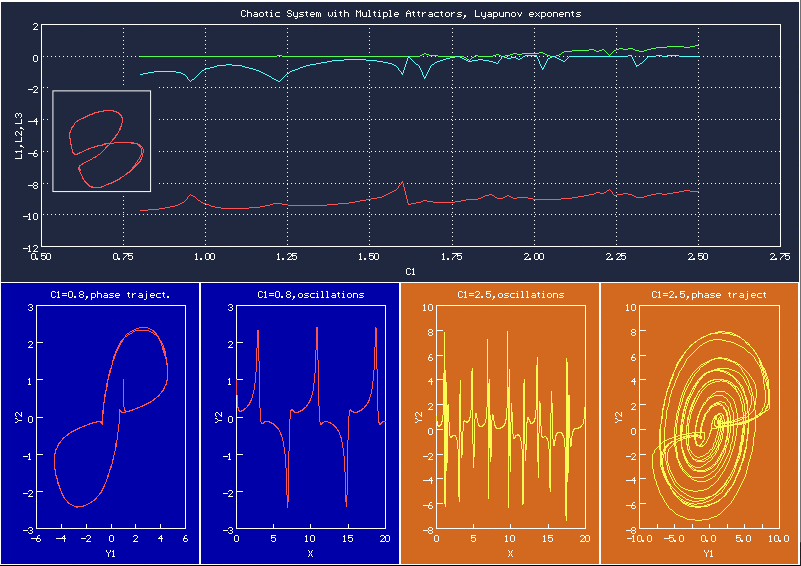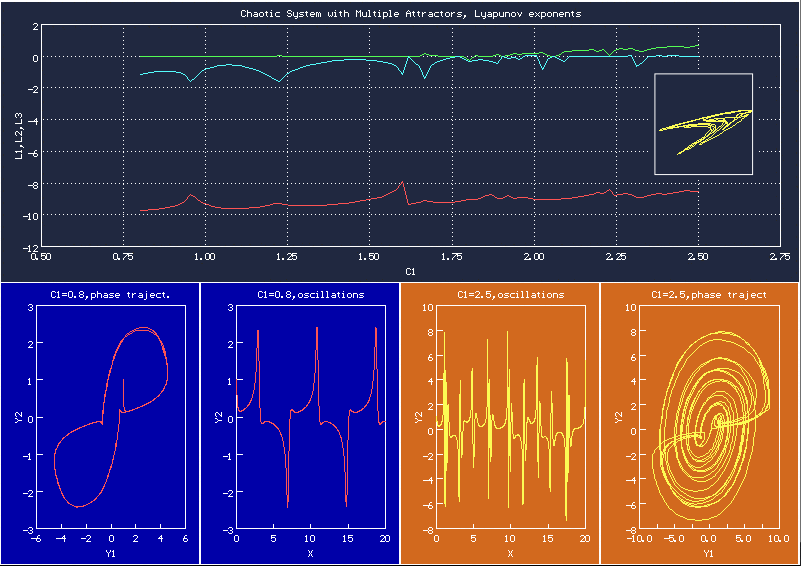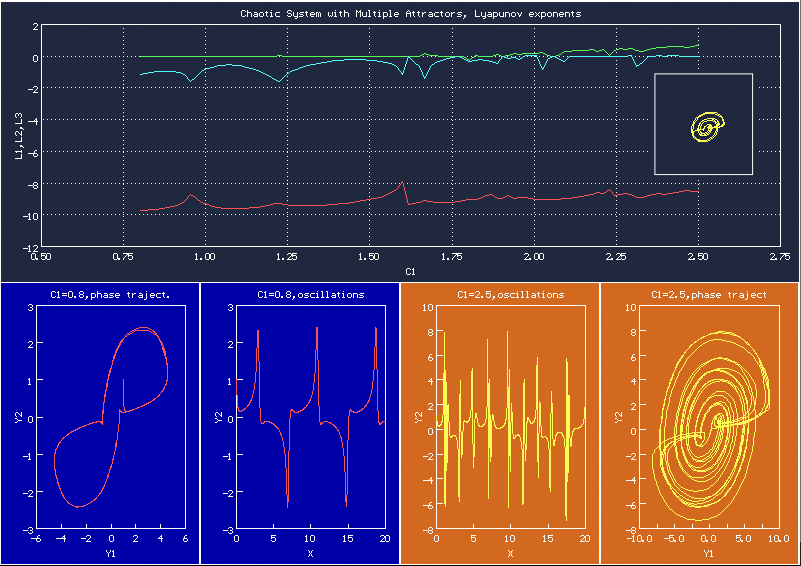
По этой картинке можно понять, где будет хаос, а где периодическое движение
Поведение динамической системы в визуальной форме
@samsergey, скажите пожалуйста, изменится ли качественно фазовый портрет рассмотренной системы, если перейти к более физической модели - избавиться от идеальности столкновения и мгновеннного обмена импульсами между шариком и столиком?
Ответ на этот вопрос уже есть в статье:
Вести себя по‑гамильтоновски и демонстрировать при этом хаотическое
поведение, будет неидеальная механическая система, в которой подавляющая
часть энергии сосредоточена в движении и потенциальных полях. Диссипация
или приток энергии извне в такие системы если и происходит, то он
пренебрежимо мал на масштабах времени, в течение которого происходит
отображение Пуанкаре. Даже если после тысяч и миллионов таких
отображений будет заметен вклад внешних возмущений и потерь, мы всё
равно будем наблюдать эффекты гамильтоновой динамики в определённом
диапазоне временных масштабов.
Если вместо столкновения использовать отталкивание, например, кулоновское, а в качестве сечения — моменты минимального сближения, то картинка исказится, но останется в целом такой-же, вместо сферы будет некоторая более сложная поверхность, но характерные паттерны гамильтонового хаоса универсальны. Если же мы добавим рассеяние энергии, то полюсы (семейства эллипттческих орбит) превратятся в фокусы (семейства спиралей). При малом рассеянии спирали будут плотными и могут успеть сформировать ряд гамильтоновых структур. Но по мере развития системы сфера будет "сдуваться", а хаотические и когерентные структуры будут исчезать.
Отличная статья, большое спасибо!
"Ничего не понятно, но очень интересно" :)
А современный ИИ и теория хаоса как-нибудь пересекаются?
Можно обучать нейросетевой ИИ на эмпирических данных связанных с поведением сложных систем, включая с нелинейной динамикой, которые пока не описываются аналитически, и предсказывать их параметры и поведение. Примеры — предсказание размерности пространства сложных нелинейных динамических систем, как пример предсказания их параметров, и предсказание траекторий в задаче 3-х тел, как пример предсказания поведения. Вот еще.
На этот вопрос хорошо в двух предыдущих комментариях ответил @phenik. Хаотические стстемы как исследуются с помощью ИИ, так и используются ими. Хаотизация и самоорганизующаяся критичность оказались в числе характерных свойств живых нейросетей в мозге. В последнее время эти свойства пытаются привить и искусственным нейросетям, полагая, что это увеличит их возможности.
Для интересующихся проблематикой нелинейной динамики журнал — Прикладная нелинейная динамика, со свободным доступом к статьям.
Спасибо автору за выбор этой темы для своих публикаций!
Самое время упомянуть константу фейгенбаума
Да, и показатели Ляпунова
Упомянем обязательно, как дело дойдëт до каскада бифуркаций Хопфа.
Не могу не привести замечательный ролик от Veritasium:
А много ли на самом деле хаоса в хаотических системах?
Рассматривая множество Мандельброта, можно заметить, что (1) оно связно; (2) оно состоит из сателлитов, соединённых тонкими нитями; (3) при увеличении любого участка нити в конце концов обнаруживается либо сателлит, либо точка ветвления.
Множество Мандельброта имеет "иглу" вдоль отрицательной части вещественной оси, которая соответствует бифуркационной диаграмме отображения x := r*x*(1-x). Каждый сателлит соответствует некоторому циклу в данном отображении. Если мы возьмём и увеличим любой участок между сателлитами, то рано или поздно обнаружим меньший сателлит, соответствующий циклу большего порядка. Т.е. получается, что зоны "хаоса" в бифуркационной диаграмме на самом деле состоят из бесконечного множества циклов (очень больших, но всё же периодических) и отдельных точек настоящего хаоса?
Различают хаотическую динамику и стохастическую. В последней нет внутренней структуры и она истинно случайна, например, в силу огромного количества степеней свободы или отсутствия памяти в системе (падение капель дождя на крышу, поток космических частиц или машин на шоссе и т.п.). Динамический хаос же, порождаемый простыми системами, типа отображения Маедельброта, действительно, можно анализировать и находить в нëм сложный порядок (самоподобные фрактальные структуры, симметрии и т. д. ). Однако эти структуры не мешает хаосу быть непредсказуемым на разумно больших временах.
У логистического отображения хаос, действительно, начинается из-за каскада удвоения периода, но этот каскад имеет в пределе хаотический режим, занимающий на бифуркационной диаграмме не отдельные точки, а большие области с канторовыми подмножествами упорядоченных областей. В этом примере через удвоение периода происходит переход от порядка к хаосу, сама же хаотическая динамика связана с перемешиванием одномерного фазового пространства "преобразованием пекаря", имеющим сплошной спектр, и происходящая в широком диапазоне параметра
.
Возможно напишу щас чушь, но самый простой пример хаоса это простые числа. Своеобразные числа-дефекты
Ну все, сжёг себе весь трафик!!( Как теперь рассказать маме, почему оплата за интернет такая огромная, так ещё и на dial-апе сидел...
Очень интересно и на всякий случай поставил плюс, но вот где-то после этих слов...
При любом анализе мы заинтересованы в минимизации числа параметров.
...стало непонятно. А зачем, собственно, минимизировать число параметров, не проще ли работать с общепонятными физическими величинами, чем с безразмерными производными параметрами?
Ну и вопрос по итогу. Значит ли это, что идеальный прыгающий на пружинке шарик является генератором случайных чисел? Можно ли использовать его (компьютерную симуляцию) для этого?
Можно, но лучше не надо. У ГПСЧ кроме, собственно, случайности, есть ещё важные характеристики — распределение и ковариация соседних значений. Современные генераторы обладают куда лучшими характеристиками нежели симуляция шарика на пружинке.
Приведение к безразмерному виду это стандартный для физики инструмент, который преследует множество практически важных задач: 1) уменьшение числа параметров без потери информации о системе, (любое многообразие всех геометрически и физически подобных решений превращается в одно решение); 2) уменьшение числа симметрий засчëт исключения тривиальных симметрий подобия, а заодно и выявление этих симметрий подобия; 3) приведение всех величин к однородным числовым значениям, с которыми возможна любая арифметика; 4) независимость от каких либо систем единиц измерения; 5) выделение характерных масштабов рассматриваемых явлений,что важно для качественного анализа задачи; 6) приведение существенной части числовых величин к порядку единицы, что очень полезно для устойчисости и точности практически всех численных алгоритмов.
Я как-то писал подробнее об этом методе на Хабре (Безразмерный воздушный шар. Утилитарная магия анализа размерностей).
В конце концов, нам ведь не важен конкретный шарик с конкретной пружинкой — сам по себе расчёт движения не является целью с которой мы приступили к решению задачи. Цель: выявить нетривиальные особенности динамики и объяснить механизм их возникновения. Поэтому с помощью перехода к безразмерным единицам, мы рассмотрели все шарики и столики с пружинками разом, оставив переменной только самую существенную и, что важно, неизменную во времени величину — полную энергию системы.
По поводу ГПСЧ, то ответ @mayorovp вполне исчерпывающий. Сгущения точек, и "дырки" в получающемся множестве портят свойства распределения чисел. Несложная нейросетка без труда выявит корреляции в этих числах и даже сможет восстановить основные детали механики, что делает этот генератор криптографически слабым. Динамический хаос неюольших размерностей для этих задач не очень подходит.
А можно ли как-то вычислить области с наибольшем количеством точек бифуркации, или градиент?
Чтобы можно было управлять "хаотичностью" системы для рекурсивных функций. Или тут только численные решения?
Может быть я утону в минусах, но есть вопрос к автору. Для понимания: я на бакалавре учился на инженера и сейчас по работе я очень далек от точных наук, но базовые вещи в голове еще сохранились.
Так вот, первый эксперимент мне кажется относительно простым с точни зрения общего понимания, потому что он о процессе, который человек может визуально наблюдать. Меня беспокоит не сам анализ, а способ подачи автором этого анализа. Самое простое, потенциальная энергия равна E = kh/mg, когда самый простой пример из физики E = mgh, в обоих случаях mg = F - сила, которая измеряется в ньютонах. В физике преподают так, что сила всегда в числителях, а у вас в знаменателе. У вас переход объясняется, но как же такое путает. Я согласен с мнением, что о комплексных вещах порой простым языком не поговорить, но все таки, как ж это путает.
Надеюсь я не один такой, но можно попросить вас упростить анализ или хотя б использовать общепринятые формулировки (я про физику, не математику)?
Для удобства математического анализа, можно все перевернуть вверх ногами, но в итоге это может закончится тем, что помимо других математиков, вас мало кто поймет.
Безразмерный парамер можно интерпретировать по-разному. 1) Как отношение характерных потенциальных сил в задаче: силы упругости к силе тяжести:
2) Как отношение потенциальных энергий
(при этом вылезает двойка, но еë можно спрятать в масштаб длины). 3) как отношение начальной высоты шарика к характерному масштабу длины
при котором сила упругости будет компенстроваться силой тяжести
.
Поскольку в дальнейшем анализе существенную роль играет энергия, как инвариант во времени, определяющий параметр многообразия на котором располагаются орбиты, и запускающий сценарий перехода к хаосу, я интерпретирую , как энергию. Вы верно заметили, что энергия шарика должна быть пропорциональна начальной высоте, вот она и пропорциональна, всë правильно. То, что
при этом оказалось в знаменателе, связано с тем, что в энергию упругости расстояние входит в более высокой степени, чем в энергию гравитации.
К сожалению, если тащить в аналих задачи метры с киллограммами, до математики дело вообще не дойдёт. А работа с безразмерными уравнениями и параметрами это и есть общепринятый в физике и инженерной механике подход. Вспомните критерии подобия Рейнольдса, Кнудсена, Релея, Грасгоффа, Архимеда, Струхаля, Галлилея, Жуковского, Прандтля... Именно на этих безразмерных числах строится инженерная гидромеханика, теплофизика, аэродинамика и многие другие прикладные разделы.
Безразмерный параметр E можно интерпретировать по-разному...
…но энергии среди этих интерпретаций нет, если лишь отношение двух потенциальных энергий.
А работа с безразмерными уравнениями и параметрами это и есть общепринятый в физике и инженерной механике подход.
Это понятно, только вот называть безразмерную величину как размерную — нельзя, если только ваша задача не состоит в том чтобы всех запутать.
Почему же нет, есть. Просто измеряется она не в Джоулях или калориях, а в безразмерных единицах. В любом случае, удвоение начальной высоты шарика увеличит ее вдвое.
Энергия не может измеряться в безразмерных единицах, любая единица в которой вы её измеряете автоматически становится её размерностью.
Какой смысл переходить к безразмерным величинам только для того чтобы наделить их размерностями обратно?
Безразмерные величины отличаются от размерных независимостью от выбранных единиц. В чем бы вы ни измеряли длину, массу, время, жесткость и ускорение в этой задаче, значение безразмерной энергии останется, неизменным. Так безразмерный радиан не зависит от того, измеряете ли вы длину окружности и радиус в сантиметрах или дюймах. Также число Рейнольдса (отношение вязких сил к силам инерции) характеризует поток жидкости и не зависит от единиц измерения размеров трубы, вязкости и скорости жидкости.
Главное достоинство безразмерных величин состоит в том, что какие бы массы и жёсткости я бы ни выбрал, переместился бы на луну, или на Юпитер, если отношение будет равно 1, я увижу ровно такое же поведение системы: такие же области хаоса и порядка, такую же структуру орбит и такие же их свойства, как показано на рисунках с
. Если же в этой реальной физической системе я как-нибудь уменьшу энергию системы вдвое (поменяю пружинку на менее жесткую, уменьшу начальную высоту, увеличу массу, или гравитацию, что заставит пружину растянуться сильнее и уменьшить скорости) то я увижу, как исчезнет хаос и колебания системы будут исключительно периодичными.
Своеобразная картина: не просто невнятный туман, а туман с каким‑то намёком на структуру. Впрочем, никакой особой закономерности в этом «сигнале» не усматриваетсяПотому что встроенный в человека спектроанализатор ориентирован на слух, а не на глаз. На слух человек может отличить шум дождя от шума из радио от фонового шума за окном и т.д.
Есть ли параллели в одной из красивейших анимаций с симуляцией света при визуализации черной дыры? Очень похоже
За статью спасибо, но можно я встану на позицию layman, как человек, знакомый только со школьной и непрофильной универской физикой и математикой? Я споткнулся в объяснениях в самом начале, можете уточнить некоторые моменты?
с нулём в точке равновесия столика (так мы исключаем из уравнений действие силы тяжести на столик)
Это как? Как выбор точки отсчёта для системы не связанной с телом позволяет исключить из уравнений действие силы тяжести на это тело? Я не понял.
попутно введя обобщённые координаты
и импульсы
системы
Что такое обобщённые координаты и откуда появилась следующие за этой фразой обозначения?
Благодарю вас за внимание и вопросы!
Когда на линейную пружинку действует постоянная потенциальная сила, то она не меняет её динамики, лишь смещая точку равновесия (речь идет о колебаниях вдали от каких-либо стенок или иных нарушений линейности). Математически это выражается в том, что в линейном дифференциальном уравнении второго порядка, легко можно исключить константу заменой переменных:
Константа здесь имеем смысл постоянного ускорения. При этом решение сместится, но все его характеристики: амплитуда, частота и затухание останутся прежними.
В аналитической механике принято рассматривать движение системы не только в пространстве, но и «во времени». Для этого к координатам всех тел системы добавляют их скорости. Такие расширенные координаты и называют обобщёнными, рассматривая их как равноправные величины. Заменой масштаба переменных можно превратить в единицу большую часть параметров задачи. Именно это происходит в заинтересовавшей вас строчке. Большие буквы — это неизвестные нам «единицы измерения» длины и скорости. Мы подбираем их так, чтобы в задаче остался один свободный параметр
. После подбора таких единиц, мы можем рассматривать не координаты и скорости, а безразмерные числа
и
. Те самые обобщённые координаты и импульсы системы.
Бардак в идеальном мире. Часть 1